Log2(x2-4) + x= log2(8(x+2))
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: \(x>-1\)
Bước quan trọng nhất là tách hàm
\(\Leftrightarrow log_2\sqrt{x+3}-2\sqrt{x+3}+\left(x+3\right)=log_2\left(x+1\right)-2\left(x+1\right)+\left(x+1\right)^2\)
Đến đây coi như xong \(\Rightarrow\sqrt{x+3}=x+1\Rightarrow x=1\)

Đáp án C
Dựa vào giả thiết, ta thấy rằng:
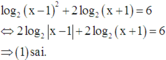
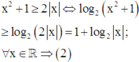
đúng.
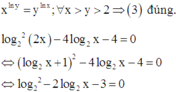
=> (4) sai. Vậy có 2 mệnh đề đúng.
Lời giải:
\(\log_2(x^2-4)+x=\log_2[8(x+2)]\)
\(\Leftrightarrow \log_2[(x-2)(x+2)]+x=\log_2[8(x+2)]\)
\(\Leftrightarrow \log_2(x-2)+\log_2(x+2)+x=\log_28+\log_2(x+2)\)
\(\Leftrightarrow \log_2(x-2)+x=3\)
Đặt \(\log_2(x-2)=t\Rightarrow x-2=2^t\Rightarrow x=2^t+2\). PT trở thành:
\(t+2^t+2=3\Leftrightarrow 2^t+t=1\)
Nếu $t>0$ thì \(2^t+t>2^0+0\Leftrightarrow 2^t+t>1\) (loại)
Nếu $t=0$ thì thỏa mãn
Nếu \(t< 0\Rightarrow 2^t+t< 2^0+0\Leftrightarrow 2^t+t< 1\) (loại)
Vậy \(t=0\Rightarrow x=2^0+2=3\)