chứng minh rằng nếu các góc ở đáy của 1 hình thang không bằng nhau thì đường chéo xuất phát từ đỉnh góc nhỏ sẽ lớn hơn đường chéo xuất phát từ đỉnh góc lớn hơn.
mọi người giúp em ạ, t2 là em phải nộp rồi ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải
Giả sử góc A < góc D. Chứng minh AC > BD
Dựng tia AE sao cho: góc DAE = góc ADC để được hình thang cân ADCE.
Ta có: góc AEC = góc DCE và AC = DE
Ta có: góc EBD > góc DCB > góc DEB
=> ED > BD => AC > BD

Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của cạnh BC.
Giả sử AM ⊥ BC. Khi đó AM là đường trung trực của đoạn thẳng BC. Suy ra AB = AC. Điều này mâu thuẫn với giả thiết AB ≠ AC. Vậy trung tuyến AM không vuông góc với BC.

Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của cạnh BC.
Giả sử AM ⊥ BC. Khi đó AM là đường trung trực của đoạn thẳng BC.
Suy ra AB = AC. Điều này mâu thuẫn với giả thiết AB ≠ AC. Vậy trung tuyến AM không vuông góc với BC.
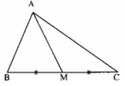
Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của cạnh BC.
Giả sử AM ⊥ BC. Khi đó AM là đường trung trực của đoạn thẳng BC. Suy ra AB = AC. Điều này mâu thuẫn với giả thiết AB ≠ AC. Vậy trung tuyến AM không vuông góc với BC.

Giả sử như AM vuông góc với BC
Xét ΔAMB vuông tại M và ΔAMC vuông tại M có
AM chung
MB=MC
Do đó: ΔAMB=ΔAMC
Suy ra: AB=AC(trái với giả thiết)

1) Đỉnh: A, B, C, D
Đáy lớn: DC
Đáy nhỏ: AB
Đường chéo: AC, BD
Cạnh bên AD, BC
2) Dùng thước thẳng hoặc compa, ta đo được: AD = BC; AC = BD
Vậy: Hai cạnh bên hình thang cân bằng nhau
Hai đường chéo hình thang cân bằng nhau.
3) Khi đặt eke vuông góc với AB ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
Vậy hai đáy của hình thang cân song song với nhau.
4) Hai góc kề một đáy của hình thang bằng nhau.
Giả sử góc A < góc D. Chứng minh AC > BD
Dựng tia AE sao cho: góc DAE = góc ADC để được hình thang cân ADCE.
Ta có: góc AEC = góc DCE và AC = DE
Ta có: góc EBD > góc DCB > góc DEB
=> ED > BD => AC > BD