Hai ô tô xuất phát cùng một lúc từ hai địa điểm AB cách nhau 102km , đi ngược chiều nhau. Ô tô chạy từ A có vận tốc 54km/h; Ô tô chạy từ B có vận tốc 48km/h.Chọn A làm mốc , gốc thời gian là lúc hai xe chuyển động ,chiều dương từ A đến B a.Phương trình toạ độ của hai xe? b. Hai xe gặp nhau ở đâu? Lúc mấy giờ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
20 tháng 1 2018
Đáp án C
Chọn trục Ox trùng với đường AB, gốc O tại A, chiều dương hướng từ A sang B, gốc thời gian là lúc hai xe xuất phát
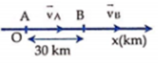
Phương trình chuyển động của ô tô chạy từ A:
(km)
Phương trình chuyển động của ô tô chạy từ B:
(km)
Khi hai ô tô gặp nhau thì
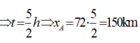
Chú ý: Khi hai vật cùng chuyển động dọc theo Ox chúng gặp nhau khi: x A = x B
ST
18 tháng 5 2022
Tổng vận tốc 2 xe là
65 + 52 = 117 (km/giờ)
Thời gian gặp nhau là
210,6 : 117 = 1.8 (giờ) = 1 giờ 48 phút
CHỗ gặp cách A số km là
52 x 1,8 = 93.6 (km)
27 tháng 10 2016
Tóm tắt
\(S_{AB}=10km\)
\(V_1=54km\)/\(h\)
\(V_2=48km\)/\(h\)
____________
\(a\)) \(t=?\)
\(b\)) \(S_{AC}=?\)
Giải
a) 
Gọi \(t_1;t_2\) lần lượt là thời gian đi của người đi vận tốc 54 km/h và 48 km/h.
Ta có:
\(S_{AC}-S_{BC}=S_{AB}=10\Rightarrow V_1.t_1-V_2.t_2=10\)
Trong đó: \(t_1=t_2=t;V_1=54km\)/\(h;V_2=48km\)/\(h\).
\(\Rightarrow10=54.t-48t=t\left(54-48\right)=6t\Rightarrow t=\frac{10}{6}=\frac{5}{3}\left(h\right)\)
b) \(\Rightarrow S_{AC}=54.\frac{5}{3}=90\left(km\right)\)
Vậy nơi 2 người gặp nhau cách điểm A là 90 km
VT
24 tháng 6 2017
Chọn đáp án C
? Lời giải:
− Phương trình chuyển động của xe A: xA = x0A + vAt = 54t (km) .
− Phương trình chuyển động của xe B: xB = x0B + vBt = 10 + 48t (km).
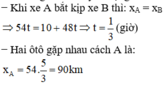
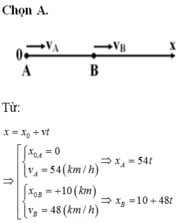
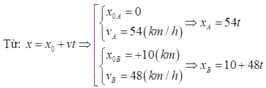
Chọn gốc tọa độ O trùng A
Chiều dương trục Ox : từ A đến B
a,Phương trình chuyển động của mỗi vật:
\(x_1=54t(km,h)\)
\(x_2=102-48t(km,h)\)
b,Khi 2 xe gặp nhau
\(x_1=x_2 \Rightarrow 54t= 102-48t\Rightarrow t=1(h)\)
Vậy thời điểm 2 xe gặp nhau là sau thời điểm xuất phát 1h
a) Phương trình tọa độ của 2 xe là:
\(x_A=54t\left(km\right)\)
\(x_B=102-48t\left(km\right)\)
b) Xl nha, mk chx nghĩ ra, bn thông cảm ạ