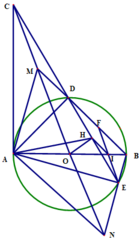
Cho điểm M thuộc đường tròn (O) đường kính AB (MA< MB). Tia phân giác của góc AMB cắt AB tại C. Qua C, vẽ đường thẳng vuông góc AB cắt các đường thẳng AM và BM lần lượt tại D và H.
a) Chứng minh hai đường thẳng AH và BD cắt nhau tại điểm N nằm trên đường tròn (O).
b) Gọi E là hình chiếu của H trên tiếp tuyến tại A của (O). Chứng minh Tứ giác ACHE là hình vuông.
c) Gọi F là hình chiếu của D trên tiếp tuyến tại B của (O).Chứng minh bốn điểm E, M, N, F thẳng hàng.
d) Gọi S1, S2 là diện tích của tứ giác ACHE và BCDF. Chứng minh \(CM^2< \sqrt{S_1S_2}\)