Cho △ABC có AB = AC. Gọi D và E là 2 điểm trên cạnh BC sao cho , BD = DE = EC. Biết AD = AE
a) Chứng minh \(\widehat{EAB}=\widehat{DAC}\)
b) Gọi M là trung điểm của BC. Chứng minh AM là phân giác của góc DAE
c) Giả sử \(\widehat{DAE}\) = 60 độ
d) Chứng minh AM ⊥ BC

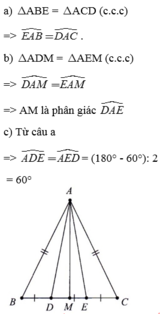
Ta có : BE=BD + ED
DC= DC+ EC
=> BE=DC
Vì AB=AC nên △ABC là △ cân
=> góc B = góc C
Xét △BAE và △CAD có
AB=AC
CD=EB
GÓC B= GÓC C
=>△BAE = △CAD (cgc )
=> EAB=DAC( 2 cạnh tương ứng ) (đpcm)
b, vì △BAE = △CAD nên AD=AE
lại có BM= BD +DM
CM=EC+EM
=> DM=EM
xét △DAM và △EAM có :
DM=EM
AD=AE
AM chung
=>△DAM = △EAM (ccc)
=>DAM=EAM
=> AM là ta phân giác góc DAE (ĐPCM)
c, không hiểu
d, xét △ BMA và △CMA có :
AB=AC
BM=MC
AM chung
=>△ BMA và △CMA(ccc)
=> BMA=BMC (2 cạnh tương ứng)
mà góc BMA +góc AMC =180o(2 góc kề bù)
=> AM ⊥ BC(ĐPCM)