Quy tắc lập bảng trong đẳng thức chứa dấu giá trị tuyệt đối là j v T-T
/x+3/ - 2x = /x-4/
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Của bạn thiếu dấu bằng .
Ta xét dấu các biểu thức trong dấu GTTĐ để khử dấu gttđ
VD1: Giải pt:
|2x−1|+|2x−5|=4−−(1)|2x−1|+|2x−5|=4−−(1)
Giải:
Ta lập bảng khử dấu gttđ: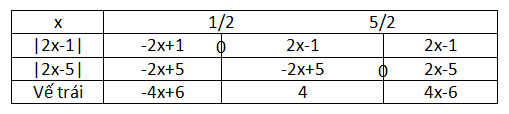
Từ đó ta xét 3 trường hợp sau:
- Xét x<12x<12
(1) trở thành −4x+6=4⇔x<12−4x+6=4⇔x<12, không phụ thuộc vào khoảng đang xét
- Xét 12≤x<5212≤x<52, (1) trở thành 4=44=4 đúng với mọi x khoảng đang xét
- Xét x≥52x≥52:
(1) trở thành 4x−6=4⇔x=524x−6=4⇔x=52, thuộc vào khoảng đang xét
Kết luận: Nghiệm của pt (1) là 12≤x≤5212≤x≤52
Mách nhỏ: Để khỏi nhầm lẫn trong việc lập bảng khử dấu giá trị tuyệt đối, các bạn hãy nhớ lấy câu: "Trái khác, phải cùng" tức là: Bên trái nghiệm của biểu thức sẽ mang dấu khác (trái) với biếu thức ta nhìn thấy, bên phải nghiệm của biểu thức sẽ mang dấu cùng với biểu thức ta nhìn thấy.
Phương pháp 2: Phương pháp biến đổi tương đương
Ta áp dụng 2 phép biến đổi cơ bản sau:
1) |a|=b⇔⎧⎪⎨⎪⎩b≥0[a=ba=−b|a|=b⇔{b≥0[a=ba=−b
2) |a|=|b|⇔[a=ba=−b|a|=|b|⇔[a=ba=−b
VD: Giải pt:
|x−1|=|3x−5|−(2)|x−1|=|3x−5|−(2)
Giải:
Áp dụng phép biến đổi 2 ta có:
(2)⇔[x−1=3x−5x−1=−3x+5(2)⇔[x−1=3x−5x−1=−3x+5
⇔⎡⎣x=2x=32⇔[x=2x=32
Kết luận: pt (2) có 2 nghiệm x1=2;x2=32x1=2;x2=32
Nhận xét: Ta có thể sử dụng phương pháp 1 để giải phương trình (2)

mày đặt câu hỏi đã đời xong mày lại trả lời thì hỏi làm gì chứ

a,|x-1|=3x+2
=>x-1=3x+2 hoặc x-1=-3x-2
x-3x=2+1 hoặc x+3x=-2+1
-2x=3 hoặc 4x=-1
x=-3/2 hoặc x=-1/4

Lời giải:
Nếu $x\geq -2$ thì PT trở thành:
$2x+4-(x+3)=4x-8$
$\Leftrightarrow x+1=4x-8$
$\Leftrightarrow 3x=9\Leftrightarrow x=3$ (tm)
Nếu $-3\leq x< -2$ thì PT trở thành:
$-(2x+4)-(x+3)=4x-8$
$\Leftrightarrow -3x-7=4x-8$
$\Leftrightarrow 7x=1\Leftrightarrow x=\frac{1}{7}$ (không thỏa mãn)
Nếu $x<-3$ thì PT trở thành:
$-(2x+4)+(x+3)=4x-8$
$\Leftrightarrow -x-1=4x-8$
$\Leftrightarrow 5x=7\Rightarrow x=\frac{7}{5}$ (không thỏa mãn)
Tập hợp giá trị $x$ thỏa mãn là $\left\{3\right\}$
bỏ dấu giá trị tuyệt đối và rút gọn biểu thức sau:
1)A=2x+4-|x-3|
2)A=-3x-2-|2x-1|
3)A=2+|x-1|+|x-2|

1) \(A=2x+4-\left|x-3\right|\)
Ta có : \(\left|x-3\right|=x-3\Leftrightarrow x-3\ge0\) hay \(x\ge3\)
\(\left|x-3\right|=-x+3\Leftrightarrow x-3< 0\) hay \(x< 3\)
* TH1 : \(A=2x+4-x+3\)
\(\Rightarrow A=x+7\)
* TH2 : \(2x+4+x-3\)
\(\Rightarrow A=3x+1\)
2) \(A=-3x-2-\left|2x-1\right|\)
Ta có : \(\left|2x-1\right|=2x-1\Leftrightarrow2x-1\ge0\) hay \(x\ge\dfrac{1}{2}\)
\(\left|2x-1\right|=-2x+1\Leftrightarrow2x-1< 0\) hay \(x< \dfrac{1}{2}\)
* TH1 : \(A=-3x-3-2x+1\)
\(\Rightarrow A=-5x-2\)
* TH2 : \(-3x-2+2x-1\)
\(\Rightarrow A=-x-3\)
3) \(A=2+\left|x-1\right|+\left|x-2\right|\)
Ta có : \(\left|x-1\right|=x-1\Leftrightarrow x-1\ge0\) hay \(x\ge1\)
\(\left|x-1\right|=-x+1\Leftrightarrow x-1< 0\) hay x < 1
\(\left|x-2\right|=x-2\Leftrightarrow x-2\ge0\) hay \(x\ge2\)
\(\left|x-2\right|=-x+2\Leftrightarrow x-2< 0\) hay \(x< 2\)
* TH1 : \(A=2+x-1+x-2\)
\(\Rightarrow A=2x-1\)
* TH2 : \(A=2+x-1-x+2\)
\(\Rightarrow A=3\)
* TH3 : \(A=2-x+1+x-2\)
\(\Rightarrow A=-x\)
* TH4 : \(A=2-x+1-x+2\)
\(\Rightarrow A=5-2x\)
1) trị tuyệt đối của x- 3 =x-3 khi x-3≥0 => x≥3
trị tuyệt đối của x-3= -x +3 khi x-3 <0 => x<3
TH1 : A = 2x + 4 -x +3 khi x ≥3
=> A = x +7
TH2 : A = 2x + 4 +x -3
=> A = 3x -1
những câu khác tương tự