Cho tam giác ABC cân tại A có BI và CE là hai đường cao
a) Chứng minh tam giác AIB = AEC
b) chứng minh tam giác AEI cân tại A
c) Chứng minh BEIC là hình thang cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 7 2021
a) Ta có: \(AD=DC=\dfrac{AC}{2}\)(D là trung điểm của AC)
\(AE=EB=\dfrac{AB}{2}\)(E là trung điểm của AB)
mà AC=AB(ΔBAC cân tại A)
nên AD=DC=AE=EB
Xét ΔADE có AE=AD(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
b) Xét ΔADB và ΔAEC có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}\) chung
AD=AE(cmt)
Do đó: ΔADB=ΔAEC(c-g-c)
c) Ta có: ΔAED cân tại A(gt)
nên \(\widehat{AED}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔAED cân tại A)(1)
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{AED}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên ED//BC(Dấu hiệu nhận biết hai đường thẳng song song)
Xét tứ giác BCDE có ED//BC(cmt)
nên BCDE là hình thang có hai đáy là ED và BC(Định nghĩa hình thang)
Hình thang BCDE(ED//BC) có BD=EC(ΔADB=ΔAEC)
nên BCDE là hình thang cân(Dấu hiệu nhận biết hình thang cân)
CM
26 tháng 8 2017
Sử dụng tính chất đường trung bình, ta chứng minh được DE//BC
27 tháng 8 2021
Xét ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
Do đó: DE//CB
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
mà \(\widehat{EBC}=\widehat{DCB}\)
nên BEDC là hình thang cân
27 tháng 8 2021
bạn ơi bạn chứng minh sai rùi ở cuối ý nếu mà 2 góc đáy bằng nhau chưa chắc đã là hình thang cân đâu chẳng hạn hình vuông 2 đáy cũng = nhau ......
nên bạn cm sai rùi sửa lại đi bạn cm 2 đường chéo bằng nhau
AH
Akai Haruma
Giáo viên
5 tháng 11 2023
Lời giải:
Vì $D$ là trung điểm $AC, $E$ là trung điểm $AB$ nên $ED$ là đường trung bình ứng với cạnh $BC$ của tam giác $ABC$
$\Rightarrow ED\parallel BC$
$\Rightarrow BEDC$ là hình thang.
Mà 2 góc ở đáy $\widehat{B}=\widehat{C}$ (do tam giác $ABC$ cân tại $A$)
$\Rightarrow BEDC$ là hình thang cân.
CM
16 tháng 6 2019
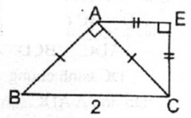
Tam giác ABC vuông cân tại A
⇒ ∠ (ACB) = 45 0
Tam giác EAC vuông cân tại E
⇒ ∠ (EAC) = 45 0
Suy ra: ∠ (ACB) = ∠ (EAC)
⇒ AE // BC (vì có cặp góc ở vị trí so le trong bằng nhau)
nên tứ giác AECB là hình thang có ∠ E = 90 0 . Vậy AECB là hình thang vuông
