rút gọn chỉ cần đáp án
K
Khách
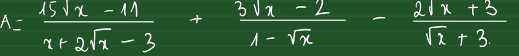
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 9 2021
\(P=\dfrac{\sqrt{x}+5\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}-2\right)}:\dfrac{x-4-x}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{6\sqrt{x}-4}{-4}=\dfrac{2-3\sqrt{x}}{2}\)
22 tháng 9 2021
\(P=\left(\dfrac{1}{\sqrt{x}-2}+\dfrac{5\sqrt{x}-4}{x-2\sqrt{x}}\right):\left(\dfrac{2+\sqrt{x}}{\sqrt{x}}-\dfrac{\sqrt{x}}{\sqrt{x}-2}\right)\)
\(=\dfrac{2\left(3\sqrt{x}-2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}:\dfrac{x-4-x}{\left(\sqrt{x}-2\right)\cdot\sqrt{x}}\)
\(=\dfrac{-3\sqrt{x}+2}{2}\)
K
24 tháng 3 2022
\(x:\dfrac{4}{5}-\dfrac{1}{16}=\dfrac{3}{4}\)
\(x:\dfrac{4}{5}=\dfrac{3}{4}+\dfrac{1}{16}\)
\(x:\dfrac{4}{5}=\dfrac{12}{16}+\dfrac{1}{16}\)
\(x:\dfrac{4}{5}=\dfrac{13}{16}\)
\(x=\dfrac{13}{16}\times\dfrac{4}{5}\)
\(x=\dfrac{13}{20}\)
NH
0
NH
0
NH
0
14 tháng 8 2021
b: Ta có: \(\left(x+5\right)^3-x^3-125\)
\(=x^3+15x^2+75x+125-x^3-125\)
\(=15x^2+75x\)
Y
11 tháng 4 2022
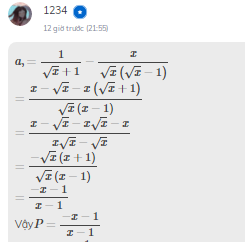
Mk ra đáp án khác với đáp án ủa bn nên bn bào sai chứ j, thật ra cả 2 đáp án đều giống nhau, do biến đổi dấu nên trở thành 2 đáp án khác nhau thôi :V
để mk lm lại phần đáp án của mk ra giống đáp án của bn nek :V
\(a,\)\(P=\dfrac{-x-1}{x-1}\)
\(\Rightarrow\dfrac{-\left(-x-1\right)}{-\left(x-1\right)}=\dfrac{x-1}{-x+1}=\dfrac{x-1}{1-x}\)
Còn câu b thì hôm qua bn ghi là \(x=\dfrac{1}{\sqrt{2}}\) chứ có pk là \(1\sqrt{2}\) đou >:V
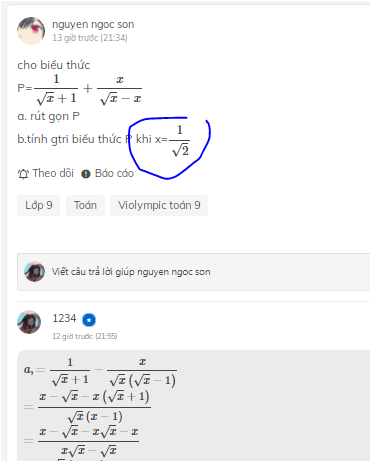
\(b,\)Thay \(x=1\sqrt{2}\) vào \(P\) ta có :
\(P=\dfrac{x-1}{1-x}\)
\(P=\dfrac{1\sqrt{2}-1}{1-1\sqrt{2}}=3+2\sqrt{2}\)
giúp mình làm phần test 4 với ạ, chỉ cần ghi đáp án thôi ạ. Đáp án cũ chưa chắc đúng nên cần gợi ý ạ
DT
Đỗ Thanh Hải
CTVVIP
31 tháng 7 2021
1 had met - came
2 will be
3 are lan and Nga doing
4 always does
5 won't get
6 has
7 were Vinh and Khoa doing
8 are there
9 are they doing
10 was
\(A=\dfrac{15\sqrt{x}-11}{x+2\sqrt{x}-3}+\dfrac{3\sqrt{x}-2}{1-\sqrt{x}}-\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}\left(x\ge0;x\ne1\right)\\ A=\dfrac{15\sqrt{x}-11-\left(3\sqrt{x}-2\right)\left(\sqrt{x}+3\right)-\left(2\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\\ A=\dfrac{15\sqrt{x}-11-3x-7\sqrt{x}+6-2x-\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\\ A=\dfrac{-5x+7\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}=\dfrac{-\left(5\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}=\dfrac{2-5\sqrt{x}}{\sqrt{x}+3}\)