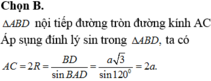Bài 15 : Cho tứ giác ABCD có ABC = ADC = 90 độ, AB = a, AD = 3a, BAD = 60 độ
Tính AC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Giải:
Kẻ hình chữ nhật \(ABCH\)
Dễ dàng tính được các độ dài: \(BD=\sqrt{10}a;BC=\sqrt{3}a,DC=\sqrt{7}a\)
\(\Rightarrow DC\perp BC\)
Ta có \(\left\{\begin{matrix} AH\perp AB\\ DA\perp AB\end{matrix}\right.\Rightarrow AB\perp (ADH)\rightarrow AB\perp DH\)
Tương tự do \(DC\perp BC,BC\perp HC\) nên \(DH\perp BC\)
\(\Rightarrow DH\perp (ABCH)\)
Theo hệ thức Pitago: \(DH=\sqrt{AD^2-AH^2}=\sqrt{6}a\)
Do đó thể tích \(ABCD\) là : \(V=\frac{S_{ABC}.DH}{3}=\frac{AB.BC.DH}{6}=\frac{\sqrt{2}a^3}{2}\)

Đáp án B.
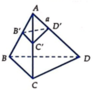
Gọi B’, C’, D’ lần lượt thuộc AB, AC, AD sao cho A B ' = A C ' = A D ' = a
Tứ diện AB’C’D’ là tứ diện đều cạnh a ⇒ V A B ' C ' D ' = a 3 2 12 (công thức cần nhớ)
Mà
V A B C D V A B ' C ' D ' = A B A B ' . A C A C ' . A D A D ' = 3.4.5 ⇒ V A B C D = 12.5. V A B ' C ' D ' = 5 a 3 2