Giải hộ mk bài 6 vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


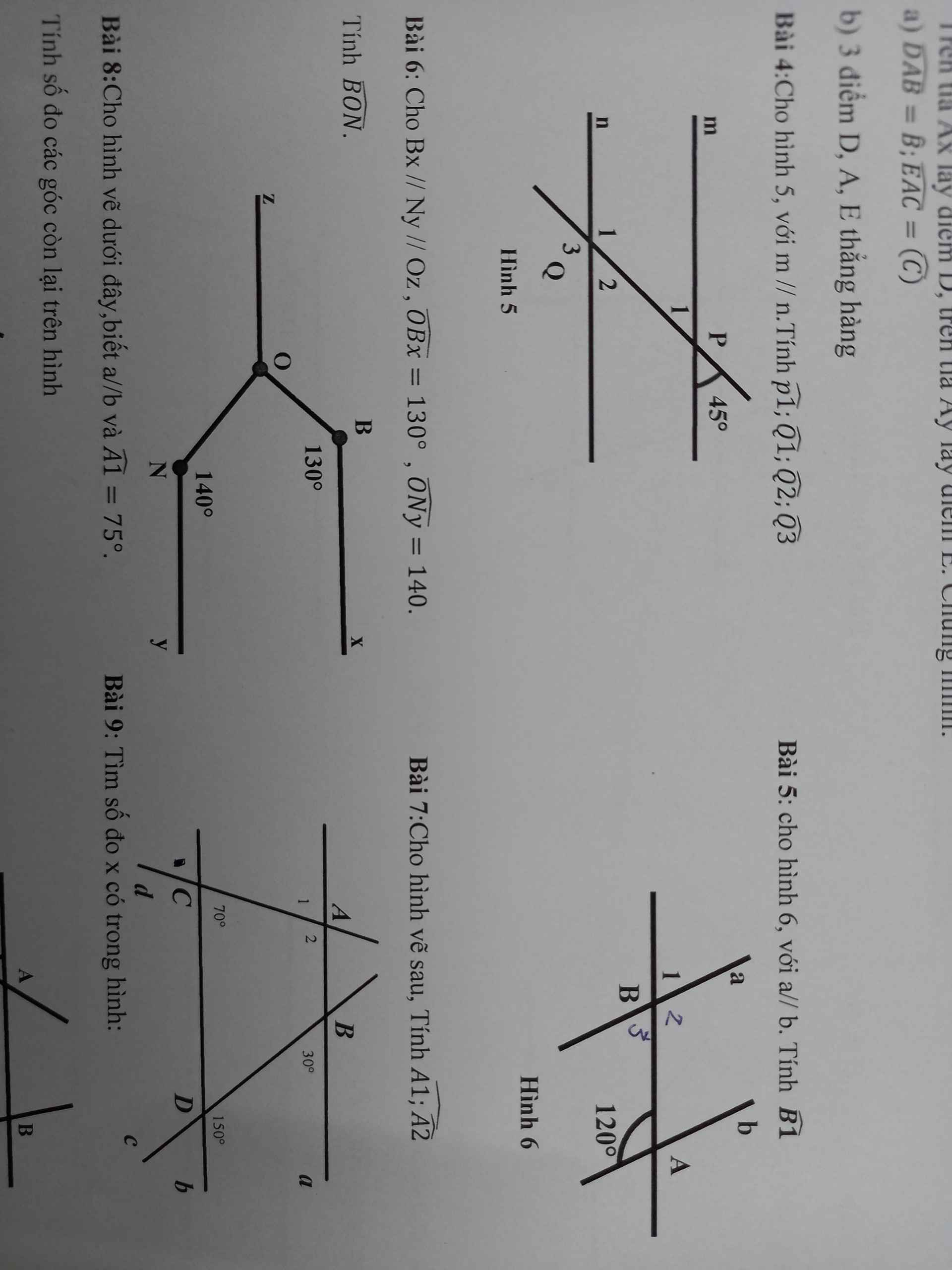
bài 5
góc BAb=1800-1200=600
mà B1=góc BAb=600(so le trong)
bài 7
có góc BDC=1800- góc BDb=1800-1500=300
=>góc BDC= góc aBD
=>a//b
=>A1=góc ACD=700
=>A2=1800-ACD=1800-700=1100


6:
a:
Xét tứ giác AEDF có
góc AED=góc AFD=góc FAE=90 độ
=>AEDF là hình chữ nhật
Xet ΔDEB vuông tạiE và ΔCFD vuông tại F có
DE=CF
EB=FD
=>ΔDEB=ΔCFD
b: Xet ΔAED vuông tại E và ΔDFA vuông tại F có
AE=DF
ED=FA
=>ΔAED=ΔDFA

f: =-1/8-7/6+3/4-1
=-3/24-28/24+18/24-1
=-31/24+18/24-1
=-13/24-1=-37/24
g: \(=6\cdot\dfrac{-8}{27}-3\cdot\dfrac{4}{9}+\dfrac{4}{3}+4\)
=-48/27+4
=108/27-48/27
=60/27
=20/9
h: \(=\left[6\cdot\dfrac{1}{9}+1+1\right]\cdot\left(-3\right)-1\)
=(2/3+2)*(-3)-1
=-2-6-1
=-3-6=-9


a) Góc xAK kề bù với góc 115 độ nên góc xAK = 650
Vì Ky song song với Ax nên góc AKy = xAk = 650 ( so le trong )
b) Vì Ky song song với Mz nên zMK + yKM = 1800 ( trong cùng phía ) => góc yKM = 350
=> góc AKM = AKy + yKM = 550 + 350 = 900 hay AK vuông góc với MK

Bài 5 hình 1: (tự vẽ hình nhé bạn)
a) Xét ΔABD và ΔACB ta có:
\(\widehat{BAD}\)= \(\widehat{BAC}\) (góc chung)
\(\widehat{ABD}\)= \(\widehat{ACB}\) (gt)
=> ΔABD ~ ΔACB (g-g)
=> \(\dfrac{AB}{AC}\) = \(\dfrac{BD}{CB}\) = \(\dfrac{AD}{AB}\) (tsđd)
b) Ta có: \(\dfrac{AB}{AC}\) = \(\dfrac{AD}{AB}\) (cm a)
=> \(AB^2\) = AD.AC
=> \(2^2\) = AD.4
=> AD = 1 (cm)
Ta có: AC = AD + DC (D thuộc AC)
=> 4 = 1 + DC
=> DC = 3 (cm)
c) Xét ΔABH và ΔADE ta có:
\(\widehat{AHB}\) = \(\widehat{AED}\) (=\(90^0\))
\(\widehat{ADB}\) = \(\widehat{ABH}\) (ΔABD ~ ΔACB)
=> ΔABH ~ ΔADE
=> \(\dfrac{AB}{AD}\) = \(\dfrac{AH}{AE}\) = \(\dfrac{BH}{DE}\) (tsdd)
Ta có: \(\dfrac{S_{ABH}}{S_{ADE}}\) = \(\left(\dfrac{AB}{AD}\right)^2\)= \(\left(\dfrac{2}{1}\right)^2\)= 4
=> đpcm
Tiếp bài 5 hình 2 (tự vẽ hình)
a) Xét ΔABC vuông tại A ta có:
\(BC^2\) = \(AB^2\) + \(AC^2\)
\(BC^2\) = \(21^2\) + \(28^2\)
BC = 35 (cm)
b) Xét ΔABC và ΔHBA ta có:
\(\widehat{BAC}\) = \(\widehat{AHB}\) ( =\(90^0\))
\(\widehat{ABC}\) = \(\widehat{ABH}\) (góc chung)
=> ΔABC ~ ΔHBA (g-g)
=> \(\dfrac{AB}{BH}\) = \(\dfrac{BC}{AB}\) (tsdd)
=> \(AB^2\) = BH.BC
=> \(21^2\) = 35.BH
=> BH = 12,6 (cm)
c) Xét ΔABC ta có:
BD là đường p/g (gt)
=> \(\dfrac{AD}{DC}\) = \(\dfrac{AB}{BC}\) (t/c đường p/g)
Xét ΔABH ta có:
BE là đường p/g (gt)
=> \(\dfrac{HE}{AE}\) = \(\dfrac{BH}{AB}\) (t/c đường p/g)
Mà: \(\dfrac{AB}{BC}\) = \(\dfrac{BH}{AB}\) (cm b)
=> đpcm
d) Ta có: \(\left\{{}\begin{matrix}\widehat{HBE}+\widehat{BEH}=90^0\\\widehat{ABD}+\widehat{ADB=90^0}\\\widehat{HBE}=\widehat{ABD}\end{matrix}\right.\)
=> \(\widehat{BEH}=\widehat{ADB}\)
Mà \(\widehat{BEH}=\widehat{AED}\) (2 góc dd)
Nên \(\widehat{ADB}=\widehat{AED}\)
=> đpcm



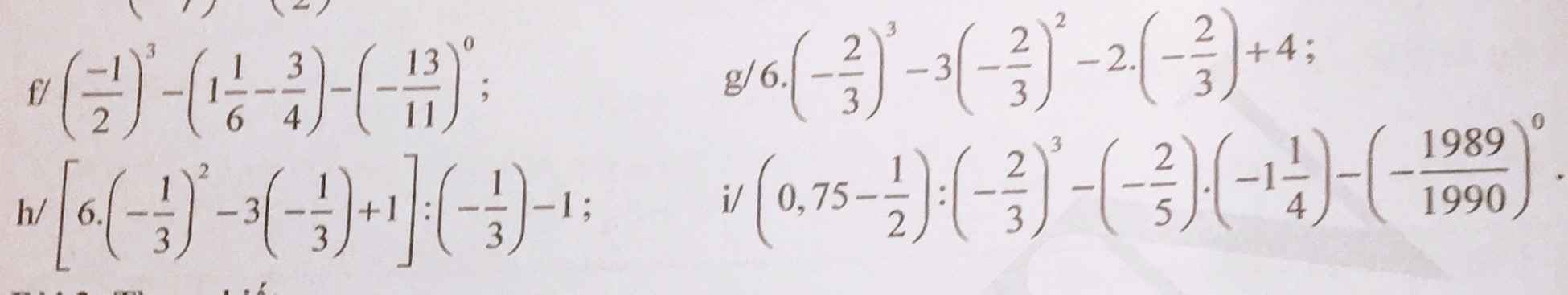


 giải hộ mình mấy bài này vs ạ !
giải hộ mình mấy bài này vs ạ !
