Giúp mình 6 câu này với ạ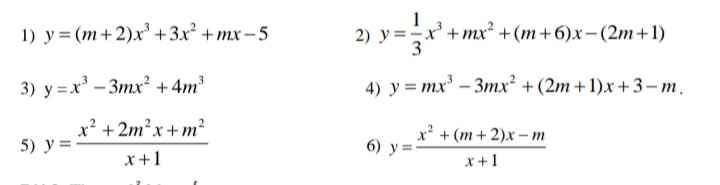 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SB
6 tháng 7 2021
mình làm những bài bn chưa lm nhé
9B
10A
bài 2
have repainted
bàii 3
ride - walikking
swimming
watch
MT
1
26 tháng 7 2022
=(-1+2)-(3+4)-(5+6)-........-(2017+2018)
=1-7-11-........-4035
=-1009
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 3 2021
ĐKXĐ: \(-2\le x\le3\)
\(\dfrac{\sqrt{-x^2+x+6}}{2x+5}-\dfrac{\sqrt{-x^2+x+6}}{x-4}\ge0\)
\(\Leftrightarrow\sqrt{-x^2+x+6}\left(\dfrac{1}{2x+5}-\dfrac{1}{x-4}\right)\ge0\)
\(\Leftrightarrow\dfrac{\left(-x-9\right)\sqrt{x^2+x+6}}{\left(2x+5\right)\left(x-4\right)}\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}-x^2+x+6=0\\\dfrac{-x-9}{\left(2x+5\right)\left(x-4\right)}\ge0\end{matrix}\right.\) \(\Leftrightarrow-2\le x\le3\)
Hoặc có thể biện luận như sau:
Ta có: \(\left\{{}\begin{matrix}2x+5>0;\forall x\in\left[-2;3\right]\\x-4< 0;\forall x\in\left[-2;3\right]\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{\sqrt{-x^2+x+6}}{2x+5}\ge0\\\dfrac{\sqrt{-x^2+x+6}}{x-4}\le0\end{matrix}\right.\) ; \(\forall x\in\left[-2;3\right]\)
Do đó nghiệm của BPT là \(-2\le x\le3\)
2H
0
DA
28 tháng 8 2021
\(\frac{1}{12}-\left(-\frac{1}{6}-\frac{1}{4}\right)\)
\(=\frac{1}{12}-\left(-\frac{2}{12}-\frac{3}{12}\right)\)
\(=\frac{1}{12}+\frac{2}{12}+\frac{3}{12}\)
\(=\frac{1}{2}\)
28 tháng 8 2021
Thanks bạn cute Jeon Koo Koo nhìu nha , tớ cảm ơn pạn rất nhìu :3
A
1
10 tháng 11 2021
\(a,m=3\Leftrightarrow y=2x+2\\ A\left(a;-4\right)\in\left(d\right)\Leftrightarrow2a+2=-4\Leftrightarrow a=-3\)
\(b,\) PT giao Ox của (d) là \(2x+m-1=0\Leftrightarrow x=\dfrac{1-m}{2}\Leftrightarrow M\left(\dfrac{1-m}{2};0\right)\Leftrightarrow OM=\dfrac{\left|1-m\right|}{2}\)
PT giao Oy của (d) là \(x=0\Leftrightarrow y=m-1\Leftrightarrow N\left(0;m-1\right)\Leftrightarrow ON=\left|m-1\right|\)
Để \(S_{OMN}=1\Leftrightarrow\dfrac{1}{2}OM\cdot ON=1\Leftrightarrow OM\cdot ON=2\)
\(\Leftrightarrow\dfrac{\left|\left(1-m\right)\left(m-1\right)\right|}{2}=2\\ \Leftrightarrow\left|-\left(m-1\right)^2\right|=2\\ \Leftrightarrow\left(m-1\right)^2=2\\ \Leftrightarrow\left[{}\begin{matrix}m=1+\sqrt{2}\\m=1-\sqrt{2}\end{matrix}\right.\)
U
1
8 tháng 6 2021
Nãy ghi nhầm =="
a)Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
Thay `m=1` vào pt ta có:
`x^2-2x-2-1=0`
`<=>x^2-2x-3=0`
`a-b+c=0`
`=>x_1=-1,x_2=3`
`=>y_1=1,y_2=9`
`=>(-1,1),(3,9)`
Vậy tọa độ gđ (d) và (P) là `(-1,1)` và `(3,9)`
b)
Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
PT có 2 nghiệm pb
`<=>Delta'>0`
`<=>1+2m+1>0`
`<=>2m> -2`
`<=>m> 01`
Áp dụng hệ thức vi-ét:`x_1+x_2=2,x_1.x_2=-2m-1`
Theo `(P):y=x^2=>y_1=x_1^2,y_2=x_2^2`
`=>x_1^2+x_2^2=14`
`<=>(x_1+x_2)^2-2x_1.x_2=14`
`<=>4-2(-2m-1)=14`
`<=>4+2(2m+1)=14`
`<=>2(2m+1)=10`
`<=>2m+1=5`
`<=>2m=4`
`<=>m=2(tm)`
Vậy `m=2` thì ....
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên