Cho hàm số \(y=x^2\). Tìm các giá trị của m để đường thẳng \(\Delta\) có phương trình \(y=x-m\) cắt đồ thị hàm số tại hai điểm phân biệt \(A\left(x_1;y_1\right)\), \(B\left(x_2;y_2\right)\) thoả mãn: \(\left(x_2-x_1\right)^4+\left(y_2-y_1\right)^4=18\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình hoành độ giao điểm: x 2 − 2 x − 2 = x + m ⇔ x 2 − 3 x − 2 − m = 0
(d) cắt (P) tại hai điểm phân biệt A, B ⇔ Δ > 0 ⇔ 17 + 4 m > 0 ⇔ m > − 17 4
Giả sử (*) có hai nghiệm x 1 , x 2 thì x 1 + x 2 = − b a = 3 x 1 . x 2 = c a = − m − 2
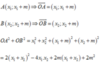
= 18 − 4 ( − 2 − m ) + 6 m + 2 m 2 = 2 m 2 + 10 m + 26 = 2 m + 5 2 2 + 27 2 ≥ 27 2 với m > − 17 4
Vậy giá trị nhỏ nhất của O A 2 + O B 2 là 27 2 khi m = − 5 2
Đáp án cần chọn là: A

Chọn C.
Phương pháp
Xét phương trình hoành độ giao điểm.
Đường thẳng cắt đồ thị (C) tại hai điểm phân biệt nếu phương trình hoành độ giao điểm có hai nghiệm phân biệt.
Cách giải:
ĐKXĐ: x ≠ 1
Xét phương trình hoành độ giao điểm x - 1 x + 1 = -x + m (*)
Với x ≠ -1 thì (*) ⇔ x - 1 = (x+1)(-x+m)
![]()
![]()
Đường thẳng y = -x + m cắt đồ thị tại hai điểm phân biệt ⇔ phương trình (**) có hai nghiệm phân biệt khác -1.
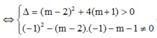
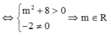
Vậy m ∈ ℝ

Phương trình hoành độ giao điểm:
\(x^2+3x=x+m^2\Leftrightarrow x^2+2x-m^2=0\)
Pt đã cho luôn có 2 nghiệm pb
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=-m^2\end{matrix}\right.\)
Do I là trung điểm đoạn AB \(\Leftrightarrow\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=-1\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{x_A+m^2+x_B+m^2}{2}=m^2-1\end{matrix}\right.\)
Mà I thuộc d'
\(\Leftrightarrow y_I=2x_I+3\Leftrightarrow m^2-1=2.\left(-1\right)+3\)
\(\Leftrightarrow m^2=2\Rightarrow m=\pm\sqrt{2}\)
\(\Rightarrow\sum m^2=4\)


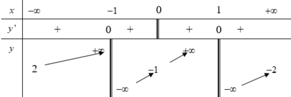

Phương trình hoành độ giao điểm là:
x^2-x+m=0
\(\text{Δ}=\left(-1\right)^2-4\cdot1\cdot m=-4m+1\)
Để phương trình có hai nghiệm phân biệt thì -4m+1>0
=>m<1/4
\(\left(x_2-x_1\right)^4+\left(y_2-y_1\right)^4=18\)
=>\(\left(x_2-x_1\right)^4+\left(x_2^2-x_1^2\right)^4=18\)
=>\(\left(x_2-x_1\right)^4\cdot\left[1+\left(x_2+x_1\right)^4\right]=18\)
\(\Leftrightarrow\left(x_2-x_1\right)^4=9\)
\(\Leftrightarrow\left(x_2-x_1\right)^2=3\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=3\)
=>1^2-4m=3
=>4m=1-3=-2
=>m=-1/2