Nung nóng 73.8 gam hỗn hợp A gồm MgCO3 và CaCO3 đến khối lượng không đổi thì chỉ còn lại 40.8 gam chất rắn.
Tính phần trăm khối lượng mỗi muối có trong hỗn hợp ban đầu.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ S ơ đ ồ p h ả n ứ n g : C a C O 3 M g O → t 0 ⏟ 30 g a m C a O M g O ⏟ 20 g a m + C O 2 ↑ ⇒ n C a C O 3 = n C O 2 = 30 - 20 44 ⇒ % m C a C O 3 = 10 . 100 44 . 30 = 75 , 76 %

Chọn A
Đề bài chỉ hỏi tỉ lệ giữa các khối lượng nên có thể lấy 90 gam hỗn hợp ban đầu và sau phản ứng còn lại
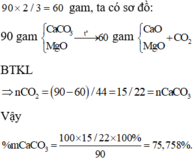

Đáp án A
Định hướng tư duy giải
Giả sử số mol CaCO3 trong hỗn hợp đầu là 1 mol
C a C O 3 → C a O + C O 2 ↑
m t r ư ớ c - m s a u = m C O 2 = m t r ư ớ c - 2 3 m t r ư ớ c
m t r ư ớ c = 3 m C O 2 = 132 g
% m C a C O 3 / h h = 75 , 76 %

Giả sử trong hỗn hợp ban đầu có 1 mol CaCO3 ⇒ nCO2 = 1
∆m = mtrước – msau ⇒ mCO2 = mtrước – 2/3mtrước = 1/3mtrước
⇒ mtrước = 3mCO2 = 3.44 = 132g
⇒ %mCaCO3 = 100 132 . 100 % = 75 , 76 % ⇒ Chọn A.

Đáp án C
Đặt số mol Na2CO3, NaHCO3 lần lượt là x, y mol → 106x + 84y= 100 (gam)
2NaHCO3 Na2CO3+ CO2+ H2O
ymol y/2 mol
→ mNa2CO3= (x+y/2).106= 69 gam
Giải hệ trên ta có x= 8/53 mol; y= 1mol
→ %mNa2CO3= 16%; %mNaHCO3= 84%

Gọi \(n_{CaCO_3}=a\left(mol\right)\) và \(n_{MaCO_3}=b\left(mol\right)\)
PTHH: \(CaCO_3\underrightarrow{t^o}CaO+CO_2\)
\(MgCO_3\underrightarrow{t^o}MgO+CO_2\)
\(\Rightarrow m_{hh}=100a+84b=18,4\)
\(n_{CO_2}=\dfrac{8,8}{44}=0,2\left(mol\right)\Rightarrow a+b=0,2\left(mol\right)\)
\(\Rightarrow a=b=0,1\left(mol\right)\)
\(\Rightarrow m_{CaCO_3}=10g;m_{MgCO_3}=8,4g\)
\(\Rightarrow\%m_{CaCO_3}=\dfrac{100\%.10}{18,4}\approx54\%;\%m_{MgCO_3}=100\%-54\%=46\%\)
MgCO3 \(\underrightarrow{to}\) MgO + CO2 (1)
CaCO3 \(\underrightarrow{to}\) CaO + CO2 (1)
Theo định luật bảo toàn khối lượng:
\(m_{hhA}=m_{cr}+m_{CO_2}\)
\(\Rightarrow m_{CO_2}=m_{hhA}-m_{cr}=73,8-40,8=33\left(g\right)\)
\(\Rightarrow n_{CO_2}=\dfrac{33}{44}=0,75\left(mol\right)\)
Gọi \(x,y\) lần lượt là số mol của MgCO3 và CaCO3
Theo PT1: \(n_{CO_2}=n_{MgCO_3}=x\left(mol\right)\)
Theo PT2: \(n_{CO_2}=n_{CaCO_3}=y\left(mol\right)\)
Ta có: \(\left\{{}\begin{matrix}84x+100y=73,8\\x+y=0,75\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=0,075\\y=0,675\end{matrix}\right.\)
Vậy \(n_{MgCO_3}=0,075\left(mol\right)\) ; \(n_{CaCO_3}=0,675\left(mol\right)\)
\(\Rightarrow m_{MgCO_3}=0,075\times84=6,3\left(g\right)\) \(\Rightarrow\%m_{MgCO_3}=\dfrac{6,3}{73,8}\times100\%=8,54\%\)
\(m_{CaCO_3}=0,675\times100=67,5\left(g\right)\Rightarrow\%m_{CaCO_3}=\dfrac{67,5}{73,8}\times100\%=91,46\%\)