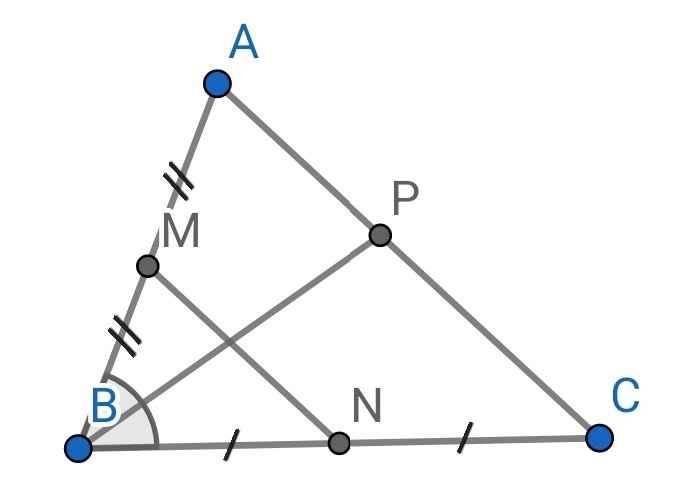
Cho tam giác ABC, M thuộc AB. N là trung điểm AC. P nằm trên MN sao cho NP=NM
a) Chứng minh MC//AP, MP=AD
b) Chứng minh PC//AM và BC=AM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 2 2023
a: Xét ΔNAM vầ ΔNCP có
NA=NC
góc ANM=góc CNP
NM=NP
=>ΔNAM=ΔNCP
b: Xét tứ giác AMCP có
N là trung điểm chung của AC và MP
=>AMCP là hình bình hành
=>PC//AM
=>PC//AB
c: Xét ΔABCcó
M,N lần lượt là trung điểm của AB,AC
nên MN là đường trung bình
=>BC=2MN
5 tháng 7 2019
a) Xét ∆ANP và ∆CMN ta có :
AN = NC
MN = NP
ANP = MNC ( đối đỉnh)
=> ∆ANP = ∆CMB (c.g.c)
=> AP = MC ( dpcm)
=> APN = NMC ( góc tg ứng)
Mà 2 góc này ở vị trí so le trong
=> AP//MC (dpcm)
b) Xét ∆AMN và ∆CPN ta có :
AN = NC
MN = NP
ANM = PNC ( đối đỉnh)
=> ∆AMN = ∆CPN (c.g.c)
=> AM = PC
=> NAM = NCP ( tg ứng)
Mà 2 góc này ở vị trí so le trong
=> AM //PC
21 tháng 7 2018
Chỉ còn vài tiếng nữa là mình nộp bài rồi, mong các bạn dành ra ít thời gian để giúp đỡ mình. Mình sẽ tích đúng cho các bạn, mình cảm ơn trước!!!!
KV
3 tháng 1
a) Do M là trung điểm của AB (gt)
⇒ AM = BM = AB : 2 = 6 : 2 = 3 (cm)
Do N là trung điểm của BC (gt)
⇒ BN = CN = BC : 2 = 8 : 2 = 4 (cm)
Ta có:
BM/AM = 3/3 = 1
BN/CN = 4/4 = 1
⇒ BM/AM = BN/CN
⇒ MN // AC (định lý Ta-lét)
b) Ta có:
AM.BC = 3.8 = 24 (cm)
AB.BN = 6.4 = 24 (cm)
⇒ AM.BC = AB.BN
c) Do BP là tia phân giác của ∠ABC (gt)
⇒ BA/BC = PA/PC (1)
Do MN // AC (cmt)
⇒ BA/BC = AM/CN (2)
Từ (1) và (2) ⇒ AM/CN = PA/PC
CW
13 tháng 6 2016
a)
Xét \(\Delta\)ANP và \(\Delta\)CNM:
NA = NC
ANP^ = CNM^ (đđ)
NP = NM
\(\Rightarrow\)\(\Delta\)ANP =\(\Delta\)CNM (c.g.c)
\(\Rightarrow\) AP = CM (2 cạnh tương ứng)
\(\Rightarrow\) NAP^ = NCM^ (2 góc tương ứng)
mà NAP^ và NCM^ sole trong
\(\Rightarrow\) AP // CM
b)
Xét \(\Delta\)ANM và \(\Delta\)CNP:
NA = NC
ANM^ = CNP^ (đđ)
NM = NP
\(\Rightarrow\)\(\Delta\)ANM = \(\Delta\)CNP (c.g.c)
\(\Rightarrow\) AM = CP (2 cạnh tương ứng)
\(\Rightarrow\)NAM^ = NCP^ (2 góc tương ứng)
mà NAM^ và NCP^ sole trong
\(\Rightarrow\) AM // CP
ồ lâu rồi ..toán lớp 7 nè ...
a/ Xét \(\Delta ANP\) và \(\Delta CNM\) có
\(AN=CN\)
\(\widehat{ANP}=\widehat{CNM}\)
\(NP=NM\)
\(\Rightarrow\Delta ANP=\Delta CNM\)
\(\Rightarrow\widehat{NAP}=\widehat{NCM}\)
\(\Rightarrow\)AP // MC
\(\Rightarrow AP=MC\)