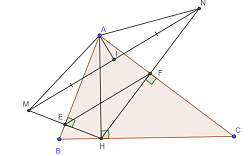
Cho tam giác ABC có đường cao AH. Kẻ EH \(\perp\)AB ( E \(\in\)AB) , kéo dài HE lấy EM = EH. Kẻ HF \(\perp\)AC = FN ( F \(\in\) AC). Gọi I là trung điểm của MN. Chứng minh:
a) AB là đường trung trực của MH và AC là trung trực của HN.
b) Tam giác AMN cân
c) EF // MN
d) AI \(\perp\)EF