toán cơ bản về phân tích đa...
Đọc tiếp
toán cơ bản về phân tích đa thức
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
0
TT
2
NT
0
AB
2
18 tháng 7 2016
x^2 + 2y^2 - 2y - 2xy + 1 = (x^2 - 2xy + y^2) + (y^2 - 2y + 1) = (x - y)^2 + (y - 1)^2
18 tháng 7 2016
\(x^2+2y^2-2y-2xy+1\)
\(=x^2-2xy+y^2+y^2-2y+1\)
\(=\left(x-y\right)^2+\left(y-1\right)^2\)
\(=\left(x-y\right)^2-\left(1-y\right)^2\)
\(=\left(x-y-1+y\right)\left(x-y+1-y\right)\)
\(=\left(x-1\right)\left(x-2y+1\right)\)
GN
0
PT
1
CM
8 tháng 4 2019
Ta để ý : x2 – 1 = (x – 1)(x + 1)
Do đó ta cần chia cả tử và mẫu của phân thức thứ nhất cho x – 1.
Mà ta có :
x5 – 1 = x5 – x4 + x4 – x3 + x3 – x2 + x2 – x + x – 1
= x4(x – 1) + x3(x – 1) + x2(x – 1) + x(x – 1) + (x – 1)
= (x – 1)(x4 + x3 + x2 + x + 1)
Do đó :
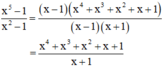
Vậy đa thức cần điền là x4 + x3 + x2 + x + 1.
SG
1
Q
19 tháng 4 2017
1. Quy tắc tìm giá trị phân số của một số cho trước:
\(-\) Muốn tìm giá trị phân số của một số cho trước ta lấy số cho trước nhân với phân số đó.
VD bài toán: Tìm \(0,6\) của \(1\dfrac{2}{5}m^2\)
2. Qui tắc tìm 1 số biết giá trị phân số của nó:
\(-\) Muốn tìm 1 số biết giá trị phân số của nó ta chia giá trị này cho phân số.
VD bài toán: \(\dfrac{3}{8}\) quả dưa hấu nặng \(2\dfrac{1}{2}\) \(kg\). Hỏi quả dưa hấu đó nặng bao nhiêu kg?
1. Quy tắc tìm tỉ số của hai số
\(-\) Tỉ số của 2 số \(a\) và \(b\) \(\left(b\ne0\right)\) là thương trong phép chia số \(a\) cho số \(b\).
\(-\) Kí hiệu: \(a\text{ }:\text{ }b\) hoặc \(\dfrac{a}{b}\)
\(-\) Muốn tìm tỉ số phần trăm của 2 số \(a\) và \(b\) ta nhân \(a\) với 100 rồi chia cho \(b\) và viết kí hiệu % vào kết quả: \(\dfrac{a.100}{b}\%\)
VD bài toán: Tìm tỉ số của 2 số \(1,25kg\) và \(\dfrac{95}{19}kg\)
PT
10
19 tháng 5 2015
Bạn dốt đến thế cơ à mà cái này còn không biết thì, bạn học lực trung bình phải không ?
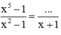
\(a,=x\left(\frac{3}{7}x+6+xy\right)\)
\(b,=\left(x+3y\right)\left(3x-6xy\right)=\left(x+3y\right).3x\left(1-2y\right)\)
\(c,=x\left(x+y\right).\left(-5\right)\left(x+y\right)=\left(x+y\right)\left[x.\left(-5\right)\right]\)
\(d,=3\left(x-y\right)+5x\left(x-y\right)=\left(x-y\right)\left(3+5x\right)\)
\(B3.a,x\left(1+6x\right)=0\)
\(Th1:x=0\)
\(Th2:1+6x=0=>x=-\frac{1}{6}\)
Vậy \(x\in\left\{0;-\frac{1}{6}\right\}\)
\(b,\left(x+3\right)\left(2-x\right)=0\)
\(Th1:x+3=0=>x=-3\)
\(Th2:2-x=0=>x=2\)
Vậy \(x\in\left\{-3;2\right\}\)
\(c,5x\left(x-2\right)+\left(x-2\right)=0\)
\(\left(x-2\right)\left(5x+1\right)=0\)
\(Th1:x-2=0=>x=2\)
\(5x +1=0=>x=-\frac{1}{5}\)
Vậy \(x\in\left\{-\frac{1}{5};2\right\}\)