xét tính chẵn lẻ của hàm số y=x5-x3+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 9 2021
TXĐ: D=R
\(y\left(-x\right)=\left(-x\right)^3-5\left(-x\right)=-x^3+5x=-\left(x^3-5x\right)=-y\left(x\right)\)
\(\Rightarrow\) Hàm lẻ
CM
5 tháng 5 2017
Đặt y = f(x) = x3 + x.
+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
+ f(–x) = (–x)3 + (–x) = –x3 – x = – (x3 + x) = –f(x)
Vậy y = x3 + x là một hàm số lẻ.
CM
17 tháng 2 2018
y = f(x) = 1/x
TXĐ: D = R \{0} ⇒ x ∈ D thì-x ∈ D
f(-x) = 1/(-x) = -1/x = -f(x)
Vậy y = f(x) = 1/x là hàm số lẻ.
CM
11 tháng 10 2018
Tập xác định D = R; ∀ x ∈ D có -x ∈ D và
f ( - x ) = 3 . ( - x ) 2 - 1 = 3 x 2 - 1 = f ( x )
Vậy hàm số đã cho là hàm số chẵn.
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 12 2020
Miền xác định của hàm là miền đối xứng
\(y\left(-x\right)=cot\left(-x\right)-sin\left(-x-1\right)=-cotx+sin\left(x+1\right)\)
\(y\left(-x\right)\ne y\left(x\right)\) mà cũng khác \(-y\left(x\right)\) nên hàm không chẵn không lẻ
PT
1
CM
16 tháng 12 2018
Đặt y = f(x) = x2 + x + 1.
+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
+ f(–x) = (–x)2 + (–x) + 1 = x2 – x + 1 ≠ x2 + x + 1 = f(x)
+ f(–x) = (–x)2 + (–x) + 1 = x2 – x + 1 ≠ –(x2 + x + 1) = –f(x)
Vậy hàm số y = x2 + x + 1 không chẵn, không lẻ.
TA
17 tháng 6 2021
Đặt `y=f(x)=x-sinx`
Có: `f(-x)=-x-sin(-x)=-x+sinx=-(x-sinx)=-f(x)`
`=>` Hàm lẻ.
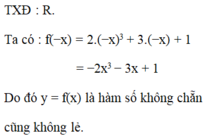
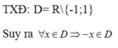
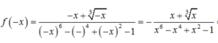
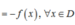
Tập xác định của hàm số là R nên cả x và -x đều nằm trong tập xác định
f(-x) = -x5 + x3 + 1
f(-x) ≠ f(x) và f(-x) ≠ - f(x)
Nên hàm số trên ko phải hàm số chẵn cũng ko phải hàm số lẻ