Cho hai điểm A, B nằm trong nửa mặt phẳng bờ là đường thẳng d. Gọi AH, BK là các đường vuông góc kẻ từ A, B đến d. Gọi C là điểm bất kì nằm giữa H và K, A’ đối xứng với A qua d. Giả sử góc ACH = góc BCK. CMR: Khi đó A’, C, B thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 10 2022
a: Xét ΔCAA' có
CH vừa là đường cao, vừa là trung tuyến
nên ΔCA'A cân tại C
=>CHlà phân giác của góc A'CA
b: góc ACH=góc BCK
=>góc A'CH=góc BCK
=>góc A'CH+góc BCH=180 độ
=>A',C,B thẳng hàng
CM
18 tháng 12 2019
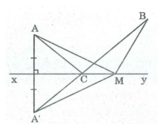
Vì A' đối xứng với A qua xy
⇒ xy là đường trung trực của AA'.
⇒ CA' = CA (t/chất đường trung trực)
MA' = MA (t/chất đường trung trực)
AC + CB = A'C + CB = A'B (1)
MA + MB = MA'+ MB (2)
Trong ∆ MA'B, ta có:
A'B < A'M + MB (bất đẳng thức tam giác) (3)
Từ (1), (2) và (3) suy ra: AC + CB < AM + MB
CM
4 tháng 12 2019
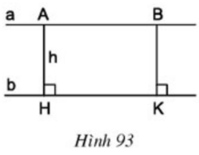
AH // BK (cùng ⊥ b) và AB // HK ⇒ tứ giác ABKH là hình bình hành
⇒ AH = BK = h
20 tháng 4 2016
)Tam giác ABC có AB=30cm, AC=40cm. Trên tia đối của tia AC lấy điểm D sao cho AD=AB. Qua A kẻ đường d vuông góc với BD. Gọi M là điểm bất kì thuộc đường thẳng d. Tìm giá trị nhỏ nhất của tổng BM+MC
Xét ΔCAA' có
CH vừa là đường cao, vừa là đường trung tuyến
nên ΔCA'A cân tại C
=>CH là phân giác của góc ACA'
=>góc A'CH=góc BCK
=>góc A'CH+góc HCB=180 độ
=>A',C,B thẳng hàng