1) Giai phuong trinh:
a) 2tanx - 3cotx - 2 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(3cos^2x-2sinx+2=0\)
\(\Leftrightarrow-3\left(1-cos^2x\right)-2sinx+5=0\)
\(\Leftrightarrow3sin^2x+2sinx-5=0\)
\(\Leftrightarrow\left(sinx-1\right)\left(3sinx+5\right)=0\)
\(\Leftrightarrow sinx=1\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)

\(\Leftrightarrow2cos^22x+3\left(\dfrac{1}{2}-\dfrac{1}{2}cos2x\right)=2\)
\(\Leftrightarrow4cos^22x-3cos2x-1=0\)
\(\Rightarrow\left[{}\begin{matrix}cos2x=1\\cos2x=-\dfrac{1}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=k2\pi\\2x=\pm arccos\left(-\dfrac{1}{4}\right)+k2\pi\\\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=\pm\dfrac{1}{2}arccos\left(-\dfrac{1}{4}\right)+k\pi\end{matrix}\right.\)

\(2cos^22x+3sin^2x=2\)
\(\Leftrightarrow-2\left(1-cos^22x\right)+3sin^2x=0\)
\(\Leftrightarrow-2sin^2x+3sin^2x=0\)
\(\Leftrightarrow sin^2x=0\)
\(\Leftrightarrow x=k\pi\)
Nguyễn Thái Sơn
\(\Leftrightarrow-2sin^22x+3sin^2x=0\)
\(\Leftrightarrow-2sin^22x+3sin^2x=0\)
\(\Leftrightarrow4sin^2x.cos^2x-3sin^2x=0\)
\(\Leftrightarrow sin^2x.\left(4cos^2x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin^2x=0\\cos^2x=\dfrac{3}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cosx=\pm\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
...

2tanx - 3cotx - 2 = 0 (Điều kiện cosx ≠ 0 và sinx ≠ 0)
Ta có
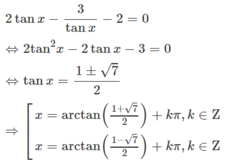

\(\Leftrightarrow\left[{}\begin{matrix}4x+10^0=x-20^0+k360^0\\4x+10^0=200^0-x+k360^0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=-30^0+k360^0\\5x=190^0+k360^0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-10^0+k120^0\\x=38^0+k72^0\end{matrix}\right.\) (\(k\in Z\))

2tanx + 3cotx = 4.
Điều kiện: cosx ≠ 0 và sinx ≠ 0. Ta có
2 tan 2 x – 4 tan x + 3 = 0
Phương trình vô nghiệm đối với tanx, do đó phương trình đã cho vô nghiệm.

a) Thay m=2 vào phương trình \(x^2+2\left(m-1\right)x-4m=0\), ta được:
\(x^2+2\cdot\left(2-1\right)x-4\cdot2=0\)
\(\Leftrightarrow x^2+2x-8=0\)(1)
\(\Delta=b^2-4ac=2^2-4\cdot1\cdot\left(-8\right)=4+32=36\)
Vì \(\Delta>0\) nên phương trình (1) có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-b-\sqrt{\Delta}}{2a}\\x_2=\dfrac{-b+\sqrt{\Delta}}{2a}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{-2-\sqrt{36}}{2\cdot1}=\dfrac{-2-6}{2}=-4\\x_2=\dfrac{-2+\sqrt{36}}{2\cdot1}=\dfrac{-2+6}{2}=2\end{matrix}\right.\)
Vậy: Khi m=2 thì phương trình \(x^2+2\left(m-1\right)x-4m=0\) có hai nghiệm phân biệt là \(x_1=-4;x_2=2\)
b) Ta có: \(x^2+2\left(m-1\right)x-4m=0\)
\(\Delta=\left[2\left(m-1\right)\right]^2-4\cdot1\cdot\left(-4\right)\)
\(\Leftrightarrow\Delta=\left(2m-2\right)^2+16>0\forall m\)
\(\forall m\) thì phương trình \(x^2+2\left(m-1\right)x-4m=0\) luôn có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-\left(2m-2\right)-\sqrt{\Delta}}{2}\\x_2=\dfrac{-\left(2m-2\right)+\sqrt{\Delta}}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{-2m+2-\sqrt{\left(2m-2\right)^2+16}}{2}\\x_2=\dfrac{-2m+2+\sqrt{\left(2m-2\right)^2+16}}{2}\end{matrix}\right.\)
Để x1 và x2 là hai số đối nhau thì \(x_1+x_2=0\)
\(\Leftrightarrow\dfrac{-2m+2-\sqrt{\left(2m-2\right)^2+16}}{2}+\dfrac{-2m+2+\sqrt{\left(2m-2\right)^2+16}}{2}=0\)
\(\Leftrightarrow-2m+2-2m+2=0\)
\(\Leftrightarrow-4m+4=0\)
\(\Leftrightarrow-4m=-4\)
hay m=1
Vậy: Khi m=1 thì phương trình \(x^2+2\left(m-1\right)x-4m=0\) có hai nghiệm phân biệt x1 và x2 thỏa mãn x1 và x2 là hai số đối nhau
a, Với m = 2 (1)<=>x^2+2x-8=0 rồi tính ra thôi
b, Để PT có 2 nghiệm PB thì
Δ=[2(m−1)]^2−4⋅1⋅(−4)Δ=[2(m−1)]2−4⋅1⋅(−4)
⇔Δ=(2m−2)^2+16>0∀m
Vì x1 và x2 là 2 số đối nhau nên x1+x2=0 <=> -2(m-1) = 0 <=> m=1
Vậy để PT có 2 nghiệm pbiet đối nhau thì m = 1
ĐK: \(x\ne\dfrac{k\pi}{2}\)
\(2tanx-3cotx-2=0\)
\(\Leftrightarrow2tanx-\dfrac{3}{tanx}-2=0\)
\(\Leftrightarrow2tan^2x-2tanx-3=0\)
\(\Leftrightarrow tanx=\dfrac{1\pm\sqrt{7}}{2}\)
\(\Leftrightarrow x=arctan\left(\dfrac{1\pm\sqrt{7}}{2}\right)+k\pi\)