Câu 24: Cho hàm số f(x)f(x) thỏa mãn 2019∫0f(x)dx=1∫02019f(x)dx=1. Tính tích phân I=1∫0f(2019x)dx.I=∫01f(2019x)dx.
A. I=0I=0
B. I=1I=1
C. I=2019I=2019
D. I=12019I=12019
Câu 25: Trong không gian Oxyz, mặt phẳng (P)(P) đi qua 2 điểm A(1;2;0)A(1;2;0), B(2;3;1)B(2;3;1) và song song với trục OzOz có phương trình là
A. x−y+1=0x−y+1=0
B. x−y−3=0x−y−3=0
C. x+z−3=0x+z−3=0
D. x+y−3=0x+y−3=0
Câu 26: Cho 4∫0f(x)dx=10∫04f(x)dx=10 và 8∫4f(x)dx=6∫48f(x)dx=6. Tính 8∫0f(x)dx.∫08f(x)dx.
A. 20
B. -4
C. 16
D. 4
Câu 27: Họ nguyên hàm của hàm số y=xsinxy=xsinx là
A. −xcosx−sinx+C−xcosx−sinx+C
B. xcosx−sin2x+Cxcosx−sin2x+C
C. −xcosx+sinx+C−xcosx+sinx+C
D. xcosx−sinx+Cxcosx−sinx+C
Câu 28: Cho số phức z=2+5iz=2+5i. Điểm biểu diễn số phức z trong mặt phẳng Oxy có tọa độ là
A. (2;−5)(2;−5)
B. (5;2)(5;2)
C. (2;5)(2;5)
D. (−2;5)(−2;5)
Câu 29: Cho 2∫−1f(x)dx=3∫−12f(x)dx=3 và −1∫2g(x)dx=1∫2−1g(x)dx=1. Tính I=2∫−1[x+2f(x)−3g(x)]dxI=∫−12[x+2f(x)−3g(x)]dx
A. 5252
B. 212212
C. 262262
D. 7272
Câu 30: Trong không gian Oxyz, cho d:x−12=y+1−1=z−32d:x−12=y+1−1=z−32. Đường thẳng nào sau đây song song với d?
A.Δ:x−2−2=y1=z−1−2Δ:x−2−2=y1=z−1−2
B. Δ:x−3−2=y+21=z−5−2Δ:x−3−2=y+21=z−5−2
C. Δ:x+1−2=y1=z−1−2Δ:x+1−2=y1=z−1−2
D. Δ:x−22=y1=z−1−2Δ:x−22=y1=z−1−2
Câu 31: Tìm họ nguyên hàm của hàm số f(x)=e5x−3.f(x)=e5x−3.
A. ∫f(x)dx=5e5x−3+C∫f(x)dx=5e5x−3+C
B. ∫f(x)dx=15e5x−3+C∫f(x)dx=15e5x−3+C
C. ∫f(x)dx=e5x−3+C∫f(x)dx=e5x−3+C
D. ∫f(x)dx=−13e5x−3+C∫f(x)dx=−13e5x−3+C
Câu 32: Tìm các số thực x,yx,y thỏa mãn: x+2y+(2x−2y)i=7−4ix+2y+(2x−2y)i=7−4i
A.x=113,y=−13x=113,y=−13
B. x=−113,y=13x=−113,y=13
C. x=1,y=3x=1,y=3
D. x=−1,y=−3x=−1,y=−3
Câu 33: Trong không gian Oxyz, phương trình đường thẳng đi qua hai điểm M(−1;0;0)M(−1;0;0) và N(0;1;2)N(0;1;2) là
A. x−11=y1=z2x−11=y1=z2
B. x+11=y1=z2x+11=y1=z2
C. x1=y−11=z+22x1=y−11=z+22
D. x1=y+11=z−22x1=y+11=z−22
Câu 34: Trong mặt phẳng tọa độ Oxy, cho điểm A(−3;4)A(−3;4) biểu diễn cho số phức z. Tìm tọa độ điểm B biểu diễn cho số phức ω=i¯¯¯zω=iz¯.
A. B(3;−4)B(3;−4)
B. B(4;3)B(4;3)
C. B(3;4)B(3;4)
D. B(4;−3)B(4;−3)
Câu 35: Cho số phức z=1+3iz=1+3i. Tìm phần thực của số phức z2z2.
A. -8
B. 8+6i8+6i
C. 10
D. −8+6i−8+6i
Câu 36: Cho tích phân I=5∫312x−1dx=aln3+bln5(a,b∈Q)I=∫3512x−1dx=aln3+bln5(a,b∈Q). Tính S=a+b.S=a+b.
A. S=0S=0
B. S=−32S=−32
C. S=1S=1
D. S=12S=12
Câu 37: Tính I=1∫0(2x−5)dx.I=∫01(2x−5)dx.
A. -3
B. -4
C. 2
D. 4
Câu 38: Trong không gian Oxyz, cho ba vectơ→a=(−2;0;1),a→=(−2;0;1), →b=(1;2;−1),b→=(1;2;−1), →c=(0;3;−4)c→=(0;3;−4). Tính tọa độ vectơ →u=2→a−→b+3→c.u→=2a→−b→+3c→.
A. →u=(−5;7;9)u→=(−5;7;9)
B. →u=(−5;7;−9)u→=(−5;7;−9)
C. →u=(−1;3;−4)u→=(−1;3;−4)
D. →u=(−3;7;−9)u→=(−3;7;−9)
Câu 39: Cho f(x)f(x) là hàm liên tục trên RR thỏa mãn f(1)=1f(1)=1 và 1∫0f(t)dt=12∫01f(t)dt=12. Tính I=π2∫0sin2x.f′(sinx)dx.I=∫0π2sin2x.f′(sinx)dx.
A. I=−1I=−1
B. I=12I=12
C. I=−12I=−12
D. I=1I=1
Câu 40: Cho phương trình z2+bz+c=0z2+bz+c=0 ẩn z và b, c là tham số thuộc tập số thực. Biết phương trình nhận z=1+iz=1+i là một nghiệm. Tính T=b+c.T=b+c.
A. T=0T=0
B. T=−1T=−1
C. T=−2T=−2
D. T=2T=2
Câu 41: Trong không gian Oxyz, viết phương trình đường vuông góc chung của hai đường thẳng d:x−22=y−33=z+4−5d:x−22=y−33=z+4−5 và d′:x+13=y−4−2=z−4−1.d′:x+13=y−4−2=z−4−1.
A. x2=y−23=z−3−1x2=y−23=z−3−1
B. x1=y1=z−11x1=y1=z−11
C. x−22=y−23=z−34x−22=y−23=z−34
D. x−22=y+22=z−32x−22=y+22=z−32
Câu 42: Biết 1+i1+i là nghiệm của phương trình zi+azi+bz+a=0(a,b∈R)zi+azi+bz+a=0(a,b∈R)ẩn z trên tập số phức. Tìm b2−a3.b2−a3.
A. 8
B. 72
C. -72
D. 9
Câu 43: Cho hình phẳng (H)(H) giới hạn bởi parabol y=ax2+1(a>0)y=ax2+1(a>0), trục tung và đường thẳng x=1x=1. Quay (H)(H)quanh trục Ox được một khối tròn xoay có thể tích bằng 2815π2815π. Mệnh đề nào dưới đây đúng?
A. 2<a<32<a<3
B. 0<a<20<a<2
C. 5<a<85<a<8
D. 3<a<53<a<5
Câu 44: Trong không gian Oxyz, cho hai đường thẳng d1:x−11=y+1−1=z2,d1:x−11=y+1−1=z2, d2:x1=y−12=z1d2:x1=y−12=z1. Đường thẳng d đi qua A(5;−3;5)A(5;−3;5) lần lượt cắt d1,d2d1,d2 tại B và C. Độ dài BC là:
A. 19
B. 3√232
C. 2√525
D. √1919
Câu 45: Trong không gian Oxyz, cho đường thẳng d:x+32=y−11=z−1−3d:x+32=y−11=z−1−3. Hình chiếu vuông góc của d trên mặt phẳng (Oyz) là một đường thẳng có vectơ chỉ phương là
A. →u=(0;1;−3)u→=(0;1;−3)
B. →u=(0;1;3)u→=(0;1;3)
C. →u=(2;1;−3)u→=(2;1;−3)
D. →u=(2;0;0)u→=(2;0;0)
Câu 46: Trong không gian Oxyz, cho điểm I(1;0;−1)I(1;0;−1) là tâm của mặt cầu (S)(S) và đường thẳng d:x−12=y+12=z−1d:x−12=y+12=z−1 cắt mặt cầu (S)(S) tại hai điểm A, B sao cho AB=6AB=6. Mặt cầu (S)(S) có bán kính R bằng:
A. √1010
B. 10
C. 2√222
D. √22
Câu 47: Cho vật thể có mặt đáy là hình tròn có bán kính bằng 1, tâm trùng gốc tọa độ (hình vẽ). Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (−1≤x≤1)(−1≤x≤1) thì được thiết diện là một tam giác đều. Tính thể tích V của vật thể đó.
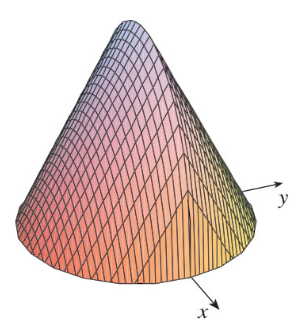
A. V=πV=π
B. V=4√33V=433
C. V=3√3V=33
D. V=√3V=3
Câu 48: Cho hai số phức z1,z2z1,z2 thỏa mãn |z1|=|z2|=|z1−z2|=1|z1|=|z2|=|z1−z2|=1. Tính |z1+z2||z1+z2|.
A. √33
B. √3232
C. 1
D. 2√323
Câu 49: Xét số phức z thỏa mãn |iz−2i−2|−|z+1−3i|=√34|iz−2i−2|−|z+1−3i|=34. Tìm giá trị nhỏ nhất của biểu thức P=|(1−i)z+1+i|.P=|(1−i)z+1+i|.
A. Pmin=√34Pmin=34
B. Pmin=√17Pmin=17
C. Pmin=√342Pmin=342
D. Pmin=13√17Pmin=1317
Câu 50: Trong không gian Oxyz, cho A(3;1;2),A(3;1;2), B(−3;−1;0)B(−3;−1;0) và mặt phẳng (P):x+y+3z−14=0(P):x+y+3z−14=0. Điểm M thuộc mặt phẳng (P) sao cho ΔMABΔMAB vuông tại M. Tính khoảng cách từ điểm M đến mặt phẳng Oxy.
A. 1 B. 5 C. 3 D. 4







=6639082
=5071011
6639082
5071011