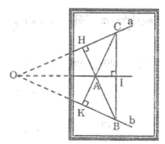
Cho 2 đường thẳng a và b cắt nhau tại O ở ngoài phạm vi tờ giấy. Hãy nêu cách đo góc nhọn tạo bởi 2 đường thẳng đã cho
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 3 2017
a) Từ A kẻ A m / / b (Am nằm trong a O b ^ )
Kẻ tia Ay là tia phân giác của a A m ^ .
Ta có: a O t ^ = 1 2 a O b ^ (Ot là tia phân giác của a O b ^ )
a A y ^ = 1 2 a A m ^ (Ay là tia phân giác của a A m ^ )
Mà a O b ^ = a A m ^ (hai góc đồng vị) ⇒ a O t ^ = a A y ^
Hai góc này lại ở vị trí đồng vị nên A y / / O t
b) Vẽ tia A z ⊥ A y
Lại có A y / / O t (theo phần a)
⇒ A z ⊥ O t (Az vuông góc với một trong hai đường thẳng song song thì phải vuông góc với đường thẳng còn lại).
CM
4 tháng 4 2019
- Kẻ AH ⊥ a kéo dài HA cắt b tại B
- Kẻ AK ⊥ b kéo dài KA cắt a tại C
- Nối BC
- Kẻ AI ⊥ BC, đường thẳng AI đi qua O
Chứng minh:
Vì tam giác OBC có hai đường cao BH và CK cắt nhau tại A nên A là trực tâm của tam giác OBC.
Khi đó OA là đường cao thứ ba nên OA ⊥ BC.
Lại có: AI ⊥ BC nên đường thẳng OA và đường thẳng AI trùng nhau ( vì qua 1 điểm nằm ngoài 1 đường thẳng ta vẽ được một và chỉ một đường thẳng vuông góc với đường thẳng cho trước).
Suy ra: đường thẳng AI đi qua O.
LL
12 tháng 12 2017
- Kẻ AH⊥aAH⊥a kéo dài, HA cắt b tại B.
- Kẻ AK⊥bAK⊥b kéo dài KA cắt a tại C.
- Kẻ AI⊥BCAI⊥BC, đường thẳng AI đi qua O.
Vì trong ∆OBC có 2 đường cao BH và CK cắt nhau tại A nên A là trực tâm của ∆OBC.
OA là đường cao thứ 3 nên OA⊥BCOA⊥BC
AI⊥BCAI⊥BC nên đường thẳng OA và đường thẳng AI trùng nhau hay đường thẳng AI đi qua O.