Nêu định lí và vẽ hình chứng minh định lí cạnh góc vuông,góc nhọn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
D
0
D
1
KT
1 tháng 10 2018
Định LÍ cạnh huyền góc nhọn: Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn tương ứng của tam giác vuông kia thì 2 tam giác đó bằng nhau.
A B C M N P
Ta có góc A + C= M + N = 90
Mà A = M (gt)
=> C=N
Xét tam giác ABC và MNP có
AB=MN ( GT)
góc C =N ( cmt )
góc A = M (gt )
=> ABC=MNP ( g c g )
Vậy tam giác vuông ABC = tam giác vuông MNP
11 tháng 11 2023
Nếu Ox,Oy là hai tia phân giác của hai góc kề bù thì Ox\(\perp Oy\)
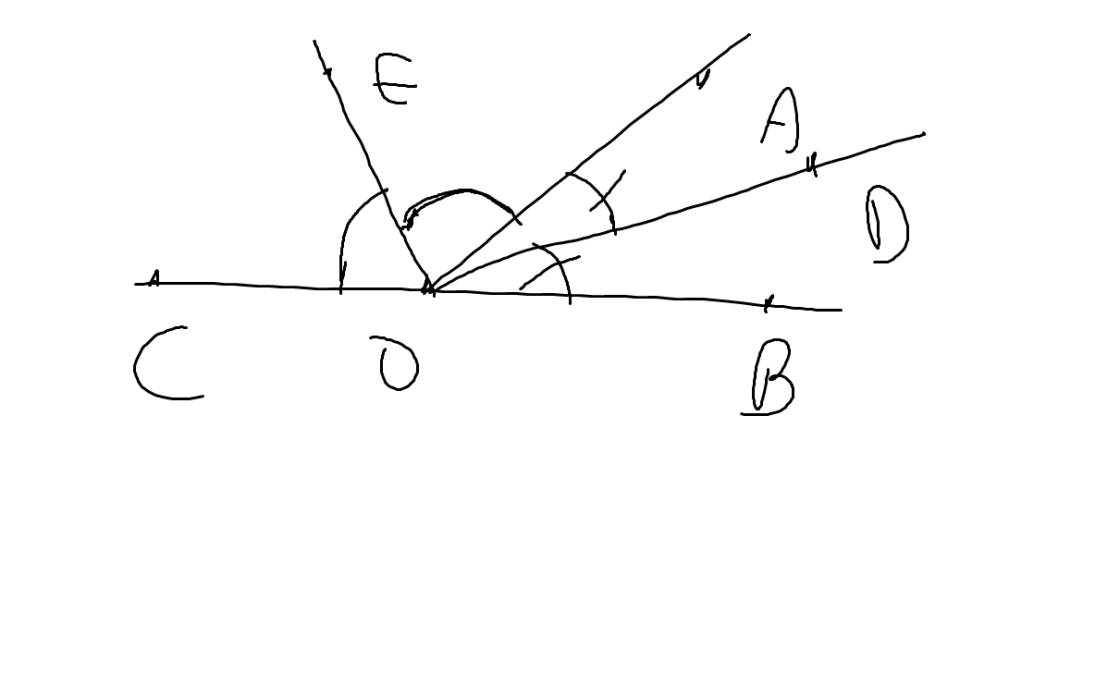
| GT | \(\widehat{AOB};\widehat{AOC}\) là hai góc kề bù OD,OE lần lượt là phân giác của \(\widehat{AOB};\widehat{AOC}\) |
| KL | OD\(\perp\)OE |
OD là phân giác của \(\widehat{AOB}\)
=>\(\widehat{AOB}=2\cdot\widehat{AOD}\)
OE là phân giác của \(\widehat{AOC}\)
=>\(\widehat{AOC}=2\cdot\widehat{AOE}\)
\(\widehat{AOB}+\widehat{AOC}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{AOE}+2\cdot\widehat{AOD}=180^0\)
=>\(\widehat{AOE}+\widehat{AOD}=90^0\)
=>\(\widehat{EOD}=90^0\)
=>OE\(\perp\)OD(ĐPCM)
7 tháng 10 2016
x x' O O y y'
GTKLgóc xOy < 90*góc x'Oy' < 90*Ox // Ox' ; Oy // Oy'góc xOy = góc x'O'y'
Vì \(Ox\) // \(Ox'\) mà \(\widehat{xOy}\) và \(\widehat{x'Ay}\) là hai góc đồng vị :
\(\Rightarrow\widehat{xOy}=\widehat{x'Ay}\) \(\left(1\right)\)
Vì \(Oy\) // \(Oy'\) mà \(\widehat{x'Ay}\) và \(\widehat{x'O'y'}\) là hai góc đồng vị :
\(\Rightarrow\widehat{x'Ay}=\widehat{x'O'y'}\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\widehat{xOy}=\widehat{x'O'y'}\)( đpcm )
Vậy : Nếu hai góc nhọn có các cặp cạnh tương ứng song song thì hai góc đó bằng nhau.
7 tháng 10 2016
x' x O O' y y'
GT KL góc xOy < 90* góc x'Oy' < 90* Ox // Ox' ; Oy // Oy' góc xOy = góc x'O'y'
Vì \(Ox\) // \(Ox'\) mà \(\widehat{xOy}\) và \(\widehat{x'Ay}\) là hai góc đồng vị :
\(\Rightarrow\widehat{xOy}=\widehat{x'Ay}\) \(\left(1\right)\)
Vì \(Oy\) // \(Oy'\) mà \(\widehat{x'Ay}\) và \(\widehat{x'O'y'}\) là hai góc đồng vị :
\(\Rightarrow\widehat{x'Ay}=\widehat{x'O'y'}\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\widehat{xOy}=\widehat{x'O'y'}\)
Vậy : Nếu hai góc nhọn có các cặp cạnh tương ứng song song thì hai góc đó bằng nhau.
17 tháng 9 2023
a)
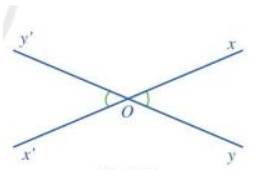
b)
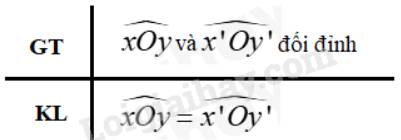
c) Vì góc xOy và x’Oy’ là hai góc đối đỉnh nên Oy và Oy’ là hai tia đối nhau; Ox và Ox’ là hai tia đối nhau
\( \Rightarrow \widehat {xOy}\) và \(\widehat {xOy'}\) là hai góc kề bù; \(\widehat {xOy'}\) và \(\widehat {x'Oy'}\) là hai góc kề bù
\( \Rightarrow \widehat {xOy} + \widehat {xOy'} = 180^\circ \); \(\widehat {xOy'} + \widehat {x'Oy'} = 180^\circ \) ( tính chất 2 góc kề bù)
\( \Rightarrow \)\(\widehat {xOy} = \widehat {x'Oy'}\) (đpcm)
17 tháng 9 2023
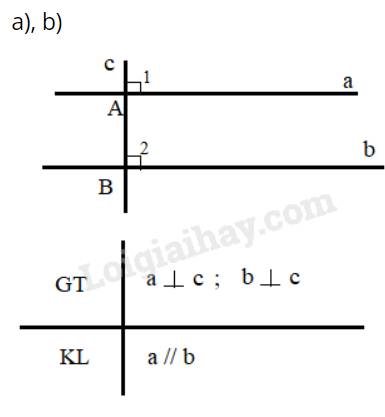
c) Giả sử có 2 đường thẳng phân biệt a,b cùng vuông góc với một đường thẳng c.
Ta có: \(\widehat {{A_1}} = \widehat {{B_2}}\), mà hai góc này ở vị trí đồng vị nên a//b (Dấu hiệu nhận biết 2 đường thẳng song song)
Như vậy, định lí trên có thể được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song.