Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Thay x=0 và y=-5 vào (d), ta được:
2(m+1)*0-m^2-4=-5
=>m^2+4=5
=>m=1 hoặc m=-1
b:
PTHĐGĐ là;
x^2-2(m+1)x+m^2+4=0
Δ=(2m+2)^2-4(m^2+4)
=4m^2+8m+4-4m^2-16=8m-12
Để PT có hai nghiệm phân biệt thì 8m-12>0
=>m>3/2
x1+x2=2m+2; x1x2=m^2+4
(2x1-1)(x2^2-2m*x2+m^2+3)=21
=>(2x1-1)[x2^2-x2(2m+2-2)+m^2+4-1]=21
=>(2x1-1)[x2^2+2x2-x2(x1+x2)+x1x2-1]=21
=>(2x1-1)(x2^2+2x2-x1x2-x2^2+x1x2-1]=21
=>(2x1-1)(2x2-1)=21
=>4x1x2-2(x1+x2)+1=21
=>4(m^2+4)-2(2m+2)+1=21
=>4m^2+16-4m-4-20=0
=>4m^2-4m-8=0
=>(m-2)(m+1)=0
=>m=2(nhận) hoặc m=-1(loại)
Lời giải:
a. Để $(d)$ đi qua $A(1;0)$ thì:
$y_A=2x_A-m+3$
$\Leftrightarrow 0=2.1-m+3=5-m$
$\Leftrightarrow m=5$
b.
PT hoành độ giao điểm:
$x^2-(2x-m+3)=0$
$\Leftrightarrow x^2-2x+m-3=0(*)$
Để $(P), (d)$ cắt nhau tại 2 điểm pb thì $(*)$ phải có 2 nghiệm pb $x_1,x_2$
Điều này xảy ra khi:
$\Delta'=1-(m-3)>0\Leftrightarrow 4-m>0\Leftrightarrow m< 4$
Áp dụng định lý Viet: $x_1+x_2=2$ và $x_1x_2=m-3$
Khi đó:
$x_1^2-2x_2+x_1x_2=-12$
$\Leftrightarrow x_1^2-(x_1+x_2)x_2+x_1x_2=-12$
$\Leftrightarrow x_1^2-x_2^2=-12$
$\Leftrightarrow (x_1-x_2)(x_1+x_2)=-12$
$\Leftrightarrow x_1-x_2=-6$
$\Rightarrow x_1=-2; x_2=4$
$m-3=x_1x_2=(-2).4=-8$
$\Leftrightarrow m=-5$ (tm)
a) (d) đi qua \(A\left(1;5\right)\Rightarrow5=2m+2m-3\Rightarrow4m=8\Rightarrow m=2\)
\(\Rightarrow y=4x+1\)
b) pt hoành độ giao điểm \(x^2-2mx-2m+3=0\)
Để (d) tiếp xúc với (P) thì pt có nghiệm kép \(\Delta=0\)
\(\Delta=\left(2m\right)^2+8m-12=4m^2+8m-12\)
\(\Rightarrow4m^2+8m-12=0\Rightarrow m^2+2m-3=0\Rightarrow\left(m-1\right)\left(m+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-3\end{matrix}\right.\)
Có d qua điểm A(1;2) và có hệ số góc k có phương trình là d; y=k(x-1)+2
Phương trình hoành độ giao điểm: 
Khi đó diện tích hình phẳng
Chọn đáp án C.
*Chú ý diện tích hình phẳng giới hạn bởi parabol
y
=
a
x
2
+
b
x
+
c
và đường thẳng d:y=mx+n có công thức tính nhanh sau 
trong đó Δ là biệt thức của phương trình hoành độ giao điểm:
a: Thay x=-1 và y=3 vào (d), ta được:
-2-m+1=3
=>-1-m=3
=>m+1=-3
hay m=-4
Bài 1:
a) Để (d) đi qua A(1;-9) thì
Thay x=1 và y=-9 vào (d), ta được:
\(3m\cdot1+1-m^2=-9\)
\(\Leftrightarrow-m^2+3m+1+9=0\)
\(\Leftrightarrow m^2-3m-10=0\)
\(\Leftrightarrow m^2-5m+2m-10=0\)
\(\Leftrightarrow m\left(m-5\right)+2\left(m-5\right)=0\)
\(\Leftrightarrow\left(m-5\right)\left(m+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m-5=0\\m+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=5\\m=-2\end{matrix}\right.\)
Vậy: Để (d) đi qua A(1;-9) thì \(m\in\left\{5;-2\right\}\)
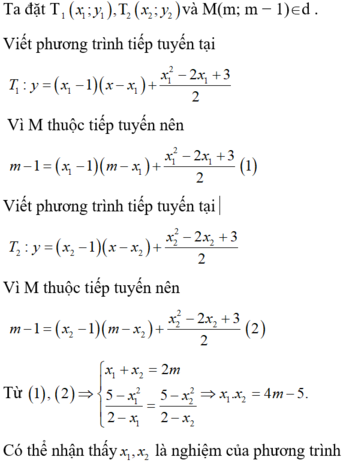
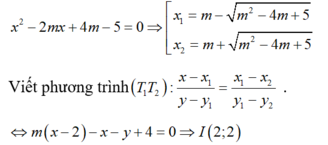
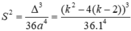
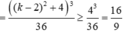
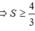
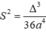
1: (d): y=kx+b
Thay x=0 và y=-1 vào (d), ta được:
\(b+k\cdot0=-1\)
=>b=-1
=>(d): y=kx-1
Phương trình hoành độ giao điểm là:
\(-x^2-kx+1=0\)
=>\(x^2+kx-1=0\)
Để trung điểm của AB nằm trên trục tung thì \(x_A+x_B=0\)
=>k=0
2: \(x_1-x_2=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\sqrt{k^2+4}\)
\(\left|x_1^3-x_2^3\right|=\left|\left(x_1-x_2\right)^3+3x_1x_2\left(x_1-x_2\right)\right|\)
\(=\left|\sqrt{\left(k^2+4\right)^3}-3k\sqrt{k^2+4}\right|\)
\(=\left|\sqrt{k^2+4}\left(k^2+4-3k\right)\right|>=2\)