Chứng minh rằng I là trung điểm của AB \(⇌\)\(\overrightarrow{IA}+\overrightarrow{IB}=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 9 2019
Giả sử \(\frac{IA}{AB}=k\Rightarrow\frac{IB}{AB}=1-k\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{IA}=-k\overrightarrow{AB}\\\overrightarrow{IB}=\left(1-k\right)\overrightarrow{AB}\end{matrix}\right.\)
\(\Rightarrow IB.\overrightarrow{IA}+IA.\overrightarrow{IB}=\left(1-k\right).AB.\left(-k\right)\overrightarrow{AB}+k.AB.\left(1-k\right)\overrightarrow{AB}\)
\(=\left(k^2-k\right)AB.\overrightarrow{AB}+\left(k-k^2\right)AB.\overrightarrow{AB}\)
\(=\left(k^2-k+k-k^2\right).AB.\overrightarrow{AB}=\overrightarrow{0}\)
B
5 tháng 9 2021
→IB+→IA−→IC−→CM=→0
=>\(\overrightarrow{IB}+\overrightarrow{IA}-\overrightarrow{IM}=\overrightarrow{0}\)
=>\(\overrightarrow{IB}+\overrightarrow{IA}=\overrightarrow{IM}\)
Đặt K là trung điểm AB
=>\(\overrightarrow{IB}+\overrightarrow{IA}=\overrightarrow{2IK}\)(T/c trung tuyến)
=>\(\overrightarrow{2IK}=\overrightarrow{IM}\)
=>K,M,I thẳng hàng
Vậy điểm M thuộc đoạn KI sao cho \(\dfrac{\overrightarrow{IK}}{\overrightarrow{IM}}=\dfrac{1}{2}\)
AH
Akai Haruma
Giáo viên
12 tháng 11 2018
Lời giải:
Áp dụng các công thức sau: \(|\overrightarrow {a}|^2=\overrightarrow{a}.\overrightarrow{a}\)
\(\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{0}\) nếu \(\overrightarrow{a}\perp \overrightarrow{b}\)
Ta có:
\(BC^2.\overrightarrow{IA}+AC^2.\overrightarrow{IB}+AB^2.\overrightarrow{IC}\)
\(=BC^2.\overrightarrow{IA}+AC^2.(\overrightarrow{IA}+\overrightarrow{AB})+AB^2.(\overrightarrow{IA}+\overrightarrow{AC})\)
\(=BC^2.\overrightarrow{IA}+\overrightarrow{IA}(AC^2+AB^2)+AC^2.\overrightarrow{AB}+AB^2.\overrightarrow{AC}\)
\(=2BC^2.\overrightarrow{IA}+AC^2.\overrightarrow{AB}+AB^2.\overrightarrow{AC}\)
\(=\overrightarrow{BC}.\overrightarrow{BC}.\overrightarrow{HA}+\overrightarrow{AC}.\overrightarrow{AC}.\overrightarrow{AB}+\overrightarrow{AB}.\overrightarrow{AB}.\overrightarrow{AC}\)
\(=\overrightarrow {BC}.\overrightarrow{0}+\overrightarrow{AC}.\overrightarrow{0}+\overrightarrow{AB}.\overrightarrow{0}=\overrightarrow {0}\)
12 tháng 11 2018
Công thức \(\left|\overrightarrow{a}\right|^2=\overrightarrow{a}.\overrightarrow{a}\)và \(\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{0}\)nếu \(\overrightarrow{a}\perp\overrightarrow{b}\) chứng minh như nào ạ ?
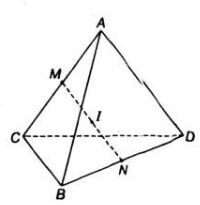
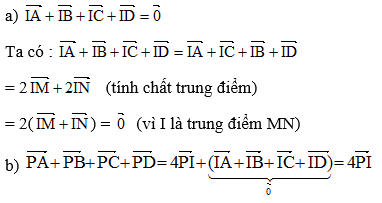
Vì I là trung điểm của AB nên IA=IB=AB/2 và I nằm giữa A và B
=>vecto IA ngược hướng với vecto IB
=>vecto IA+vecto IB=vecto 0