Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét tứ giác AHFK có
góc AHF=góc AKF=góc KAH=90 độ
=>AHFK là hình chữ nhật
b: Gọi O là giao của AC và BD, I là giao của AF và HK
AHFK là hình chữ nhật
=>I là trung điểm chung của AF và HK
ABCD là hình chữ nhật
=>O là trung điểm chung của AC và BD
Xét ΔAFC có I,O lần lượt là trung điểm của AF,AC
=>IO là đường trung bình
=>IO//FC và IO=FC/2
=>IO//FE và IO=FE
Xét tứ giác IFEO có
IO//FE
IO=FE
=>IFEO là hình bình hành
=>IF//OE
=>AF//BD
a) F H A ^ = H A K ^ = A K F ^ = 90 0
Þ AHFK là hình chữ nhật.
b) Gọi là giao điểm của AC và BD. Chứng minh OE là đường trung bình của DACF
Þ AF//OE
Þ AF/BD
c) Gọi I là giao điểm của AF và HK.
Chứng minh
H 1 ^ = A ^ 1 ( H 1 ^ = A 2 ^ = B 1 ^ = A 1 ^ ) ⇒ K H / / A C mà KH đi qua trung điểm I của AF Þ KH đi qua trung điểm của FC.
Mà E là trung điểm của FC Þ K, H, E thẳng hàng
a) F H A ^ = H A K ^ = A K F ^ = 90 0
Þ AHFK là hình chữ nhật.
b) Gọi là giao điểm của AC và BD. Chứng minh OE là đường trung bình của DACF
Þ AF//OE
Þ AF/BD
c) Gọi I là giao điểm của AF và HK.
Chứng minh
H 1 ^ = A ^ 1 ( H 1 ^ = A 2 ^ = B 1 ^ = A 1 ^ ) ⇒ K H / / A C mà KH đi qua trung điểm I của AF Þ KH đi qua trung điểm của FC.
Mà E là trung điểm của FC Þ K, H, E thẳng hàng
a) Để chứng minh BD = 2AO, ta có thể sử dụng định lý Thales và các quy tắc về tỉ lệ đồng dạng. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
b) Để chứng minh I là trung điểm của KH, ta có thể sử dụng các quy tắc về đường thẳng song song và đồng quy. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
c) Để chứng minh tứ giác AIEO là hình bình hành, ta có thể sử dụng các quy tắc về đường chéo và cạnh đối. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
d) Để chứng minh I, K, E thẳng hàng, ta có thể sử dụng các quy tắc về đường thẳng và góc vuông. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
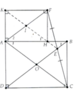
Bạn tự vẽ hình nha!
a) Do ABCD là hình chữ nhật ⇒ Góc BAD = 90 độ. Mà góc BAD+góc KAH = 180 độ (2 góc kề bù) ⇒ 90 độ + góc KAH = 180 độ ⇒ Góc KAH = 90 độ.Vì FH vuông góc với AB ( giả thiết); FK vuông góc với AD (giả thiết) ⇒ Góc FKA= 90 độ và góc FHA= 90 độ. Xét tứ giác AHFK có 3 góc vuông ⇒ Tứ giác AHFK là hình chữ nhật.
b) Nối A với C, gọi I là giao điểm của 2 đường chéo AC và BD. Do I là giao điểm của 2 đường chéo của hình chữ nhật ⇒ I là trung điểm của AC (tính chất của hình chữ nhật). Vì EF= EC (giả thiết) ⇒ E là trung điểm của FC. Xét tam giác ACF có E là trung điểm của FC; I là trung điểm của AC ⇒ EI là đường trung bình của tam giác ACF ⇒ EI song song với AF (Tính chất đường trung bình của tam giác).