Question

[Trần Phương Thảo]

bài 1

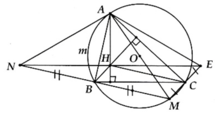
cho \(\Delta ABC\) nội tiếp đường tròn tâm O, H là trực tâm, D đối xứng với A qua O

a. chứng minh tứ giác HCDB là hình bình hành

b chứng minh: \(\overrightarrow{HA}+\overrightarrow{HD}=2\overrightarrow{HO};\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=2\overrightarrow{HO}\);\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OH}\)

c.Gọi G là trọng tâm của \(\Delta ABC\). Chứng minh \(\overrightarrow{OH}=3\overrightarrow{OG}\). Từ đó kết luận gì về 3 điểm G, O, H

bài 2

\(\Delta ABC\) là tam giác gì nếu nó thỏa mãn một trong các điều kiện sau

a.\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\left|\overrightarrow{AB}-\overrightarrow{AC}\right|\)

b. \(\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\perp\left(\overrightarrow{AB}+\overrightarrow{CA}\right)\)