A B D E O C Chứng minh...
Đọc tiếp
Chứng minh OC//OE:OC//AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22math1ed582716bfb4738ccd92405301%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%227.5%22%20y%3D%2216%22%3E%26%23x2206%3B%3C%2Ftext%3E%3C%2Fsvg%3E)
ABC đều
b) Đường vuông góc với OB tại O cắt AC tại D. Đường vuông góc với OC tại O cắt AB tại E. Chứng minh tứ giác ADOE là hình thoi
c) Chứng minh DE là tiếp điểm của đường tròn (O)
17 tháng 5 2023
a: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
Xét ΔOBA vuông tại B có sin BAO=OB/OA=1/2
nên góc BAO=30 độ
=>góc BAC=60 độ
=>ΔBAC đều
b: Xét tứ giác OEAD có
OE//AD
OD//AE
AO là phân giác
=>OEAD là hình thoi
CM
22 tháng 3 2018
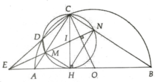
a, Tứ giác CMHN là hình chữ nhật
b, Ta có
O
C
A
^
=
O
A
C
^
C B A ^ = A C H ^ ; A C H ^ = C M N ^
=> O C A ^ + C M N ^ = 90 0
Vậy OC ⊥ MN
c, Ta có ∆IOC có E là trực tâm suy ra IN đi qua M và E (đpcm)
d, Ta có E M A ^ = C M N ^ ; C M N ^ = C B A ^ => ∆EMA:∆ENB
Tương tự ∆EMH:∆EHN => EM.EN = E H 2 ngoài ra , ∆EHC vuông tại H có HD là đường cao
=> E H 2 = ED.EC. Từ đó ta có đpcm
26 tháng 9 2017
a)Nối F với D : E với D ta có:
Xét tam giác FBC ta có
D là trung điểm BC(1)
Góc BFC=90 (2)
Từ (1)(2)=>FD là trung tuyến của tam giác FBC
=>BD=CD=DF(*)
Chứng minh tương tự tam giác EBC
=>DE=DC=DB(**)
Từ (*)(**)=>BD=CD=DF=DE=(1/2BC)
=>B;F;E;C thuộc đừng tròn
=>D là tâm của đường tròn
B) Do B;H;E nằm trên cùng 1 đừng thẳng => H ko thuộc đừng tròn
=>B;H;E;c ko thuộc đừng tròn
11 tháng 3 2022
a) Xét (O):
AB là tiếp tuyến; B là tiếp điểm (gt). \(\Rightarrow\widehat{ABO}=90^o.\)
AC là tiếp tuyến; C là tiếp điểm (gt). \(\Rightarrow\widehat{ACO}=90^o.\)
\(\Rightarrow\) 4 điểm A, B, O, C cùng thuộc một đường tròn đường kính AO.
b) Xét (O):
\(\widehat{ACD}=\widehat{AEC}\) (Góc tạo bởi tia tiếp tuyến và dây; góc nội tiếp cùng chắn \(\stackrel\frown{CD}\)).
Xét \(\Delta ACD\) và \(\Delta AEC:\)
\(\widehat{ACD}=\widehat{AEC}\left(cmt\right).\)
\(\widehat{CAD}chung.\)
\(\Rightarrow\Delta ACD=\Delta AEC\left(g-g\right).\)
\(\Rightarrow\dfrac{AC}{AE}=\dfrac{AD}{AC}.\\ \Rightarrow AC^2=AD.AE.\)