Kết luận nào sau đây đúng về GTLN và GTNN của hàm số y=căn(x-x^2)
A. Có GTLN và có GTNN
B. Có GTLN và k có GTNN
C. có GTNN và k có GTLN
D.Không có GTNN và GTLN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
22 tháng 8 2021
Lời giải:
\(y'=\frac{5-x}{\sqrt{(x^2+5)^3}}=0\Leftrightarrow x=5\)
Lập bảng biến thiên với các chốt $x=-\infty, x=5; x=+\infty$ ta thấy hàm số có GTLN tại $x=5$
Đáp án D.
CM
3 tháng 7 2019
Chọn C.
Phương pháp:
Tìm TXĐ của hàm số, sau đó tìm GTLN, GTNN của hàm số sau đó chọn đáp án đúng.
Cách giải:
15 tháng 3 2017
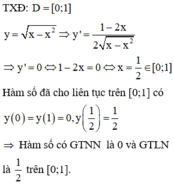
Vì | x -3 | > hoặc = 0
Suy ra : |x-3|+50 >hoặc =50
Vì A nhỏ nhất suy ra | x-3 | +50 =50
Suy ra x-3 =0
Suy ra x=3
Vậy GTNN của A = 50 khi x=3
Chọn A