Giải dùm mình gấp, mình thanks mấy bạn trước 😘😘
Xác định a,b để hàm số y=ax+b đi qua điểm D(3;1) và tạo với các trục tọa độ một tam giác có diện tích lớn nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(d) đi qua M(2;3) và N(5;4)
=>Ta có hệ phương trình:
2a+b=3 và 5a+b=4
=>a=1/3 và b=7/3

a47b chia hết cho 5 => b=0 hoặc 5
b = 0 thì a470 chia hết cho 9 => a+4+7+0 chia hết cho 9
=> a+11 chia hết cho 9 => a=7 ( vì 0 < a < = 9 )
b = 5 thì a475 chia hết cho 9 => a+4+7+5 chia hết cho 9
=> a+16 chia hết cho 9 => a=2 ( vì 0 < a < = 9 )
Vậy ............
Tk mk nha

a và b thỏa mãn hệ phương trình :
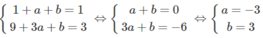
c và d thỏa mãn hệ phương trình:
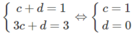
Lời giải:
ĐTHS đi qua $D(3;1)$ nên: \(1=3a+b\Rightarrow b=1-3a\)
Vậy $y=ax+1-3a$
Ta có:
\((y)\cap Ox=A(\frac{3a-1}{a};0)\)
\((y)\cap Oy=B(0; 1-3a)\)
Như vậy, đths tạo với các trục tọa độ một tam giác có diện tích là:
\(S_{OAB}=\frac{|OA||OB|}{2}=\frac{|\frac{3a-1}{a}||1-3a|}{2}\)
\(=\frac{(3a-1)^2}{2|a|}\)
Biểu thức trên không có max. Không tồn tại $a,b$ để diện tích max.
Cái dấu sau chữ y và trước ox là gì vậy