Câu 1: Hai vật xuất phát từ A và B cách nhau 340m, chuyển động cùng chiều theo hướng từ A đến B. Xe thứ nhất đi với vận tốc 5m/s, xe thứ hai có vận tốc bằng một nữa vận tốc xe thứ nhất. Tính:
A) Khoảng cách của hai xe sau 100s
B) Hai vật gặp nhau sau bao lâu và vị trí gặp nhau cách A bao nhiêu
Câu 2: Một vật chuyển động trên đoạn đường AB dài 240m. Trong nửa đoạn đường đầu tiên nó đi với vận tốc v1=5m/s, trong nửa đoạn đường sau nó đi với vận tốc v2=6m/s. Tính thời gian vật chuyển động hết quãng đường AB?

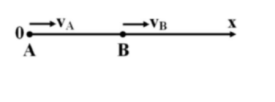 Cách 1: Từ:
Cách 1: Từ: 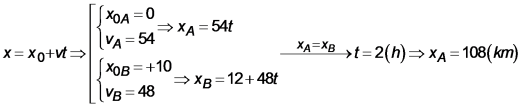 Cách 2: Mỗi giờ xe A đi được nhiều hơn xe B là 54 – 48 = 6km. Muốn xe A đi được nhiều hơn xe B là 12 km thì phải cần thời gian: 12/6 = 2h. Lúc này, xe A đi được: AC = 54.2 = 108 km.
Cách 2: Mỗi giờ xe A đi được nhiều hơn xe B là 54 – 48 = 6km. Muốn xe A đi được nhiều hơn xe B là 12 km thì phải cần thời gian: 12/6 = 2h. Lúc này, xe A đi được: AC = 54.2 = 108 km.
Câu 2:
Ta có:
\(S_{AB}=240m\Rightarrow S_1=S_2=240:2=120m\)
\(v_1=5m/s\)
\(v_2=6m/s\)
\(t_1=?\)
\(t_2=?\)
\(t=?\)
Thời gian chuyển động trên nửa quãng đường đầu là:\(t_1=S_1:v_1=120:5=24\left(s\right)\)
Thời gian chuyển động trên nửa quãng đường sau là:
\(t_2=S_2:v_2=120:6=20\left(s\right)\)
Thời gian chuyển động hết quãng đường AB là:
\(t_1+t_2=24+20=44\left(s\right)\)
Câu 1:
Gọi t là thời gian chuyển động của 2 vật
Quãng đường vật A đi được là \(S_1=v_1.t=5t\)
vì 2 vật chuyển động cùng chiều từ A đến B nên lúc đầu vật B cách vật A 1 khoảng \(S_0=340\)
Vật B cách vật A đoạn đường là:\(S_2=S_0+v_2.t=340+\left(\dfrac{v_1}{2}\right)t=340+2,5t\)
\(\)Khoảng cách giữa hai xe là:
\(\Delta s=s_2-s_1=340+2,5t-5t=340-2,5t\)
Sau 100s là: \(340-2,5.100=90\left(m\right)\)
b, hai xe gặp nhau sau:
\(S_1=S_2\Leftrightarrow5t=340+2,5t\Leftrightarrow2,5t=340\Leftrightarrow t=136\left(s\right)\left(1\right)\)
vị trí gặp cách A là:
Từ \(\left(1\right)\Rightarrow s_1=5t=5.136=680\left(m\right)\)