một ca nô xuất phát từ điểm A trên một khúc sông thẳng AB= 8km và chạy xuôi dòng. Cùng lúc đó, tại A một bè gỗ cũng bắt đầu trôi xuôi dòng. Ca nô chạy đến B thì quay lại chạy ngược dòng, sau 48 phút tính từ lúc xuất phát ở A, ca nô gặp lại bè lần thứ nhất tại C, với BC= 6,4km. Coi nước chảy đều, vận tốc của ca nô so với nước là không đổi. Bỏ qua thời gian ca nô quay đầu, kích thước của ca nô và của...
Đọc tiếp
một ca nô xuất phát từ điểm A trên một khúc sông thẳng AB= 8km và chạy xuôi dòng. Cùng lúc đó, tại A một bè gỗ cũng bắt đầu trôi xuôi dòng. Ca nô chạy đến B thì quay lại chạy ngược dòng, sau 48 phút tính từ lúc xuất phát ở A, ca nô gặp lại bè lần thứ nhất tại C, với BC= 6,4km. Coi nước chảy đều, vận tốc của ca nô so với nước là không đổi. Bỏ qua thời gian ca nô quay đầu, kích thước của ca nô và của bè.
a) Tính vận tốc của dòng nước và vận tốc của ca nô khi xuôi dòng.
b) Giả sử sau khi gặp bè, ca nô quay lại chạy xuôi, tới B lại chạy ngược, gặp bè lại chạy xuôi,... cứ như vậy chớp đến khi ca nô và bè gặp nhau ở B. Tình tổng thời gian chạy của ca nô.(Team Lý giải hộ nha)
bạn giải nốt phương trình nhé
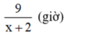
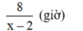
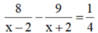
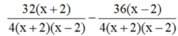
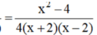
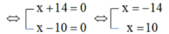
Đổi 48p'=0,8h
a. Thời gian chạy của ca nô bằng thời gian trôi của bè, vận tốc dòng nước
\(v_n=v_b=\dfrac{AC}{t}=\dfrac{8-6,4}{0,8}=2\)(km/h)
Gọi vận tốc của ca nô so với nước là \(v_0\) , vận tốc ca nô khi xuôi dòng và ngược dòng là \(v_1\) và \(v_2\)
\(\Rightarrow v_1=v_0+v_n;v_2=v_0-v_n\)
Thời gian chạy xuôi dòng \(t_1=\dfrac{AB}{v_1}=\dfrac{AB}{v_0+v_n}\left(1\right)\)
Thời gian chạy ngược dòng \(t_2=\dfrac{AB}{v_2}=\dfrac{AB}{v_0-v_n}\left(2\right)\)
Theo bài ra ta có \(t_1+t_2=h\)
Từ (1),(2),(3) ta có:
\(\dfrac{AB}{v_0+v_n}+\dfrac{CB}{v_0-v_n}=\dfrac{8}{v_0+2}+\dfrac{6,4}{v_0-2}\Rightarrow v^2_0-18v_0=0\Rightarrow v_0=18km/h\)Khi xuôi dòng: \(v_1=20\left(km/h\right)\)
b, Tổng thời gian chạy của ca nô chính là thời gian bè trôi từ A đến B:\(t_3=\dfrac{AB}{v_n}=\dfrac{8}{2}=4h\)
ủng hộ tui quá nhỉ @Trịnh Công Mạnh Đồng