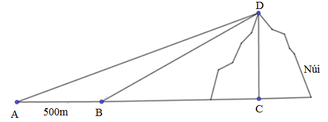
Tính chiều cao của một ngọn núi (làm tròn đến mét), biết tại hai điểm A, B cách nhau 500m,người ta nhìn thấy đỉnh núi với góc nâng lần lượt là 34°và 38°
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 5 2018
Ta có hình vẽ minh họa với D A C ^ = 34 0 ; D B C ^ = 38 0
Xét tam giác vuông ADC vuông tại C có:
Xét tam giác vuông BDC vuông tại C có:
Có:
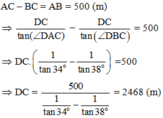
Vậy độ cao của ngọn núi là 2468m
Đáp án cần chọn là: D
23 tháng 7 2023
Gọi hai điểm trên mặt đất là A,B
Đỉnh của ngọn núi là C
Theo đề, ta có: góc A=40 độ; góc B=32 độ; AB=1km
góc C=180-40-32=108 độ
Xét ΔABC có AB/sinC=AC/sinB=BC/sinA
=>AC\(\simeq\)0,56(km); CB\(\simeq\)0,68(km)
S CAB=1/2*0,56*0,68*sin108
\(\simeq0,18\left(km^2\right)\)
Chiều cao của ngọn núi là;
0,18*2:1=0,36(km)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Tam giác ABC vuông tại B nên ta có: \(\tan C = \frac{{AB}}{{CB}} \Leftrightarrow AB = \tan {32^ \circ }.(1 + x)\)
Tam giác ADB vuông tại B nên ta có: \(\tan D = \frac{{AB}}{{DB}} \Leftrightarrow AB = \tan {40^ \circ }.x\)
\(\begin{array}{l} \Rightarrow \tan {32^ \circ }.(1 + x) = \tan {40^ \circ }.x\\ \Leftrightarrow x.(\tan {40^ \circ } - \tan {32^ \circ }) = \tan {32^ \circ }\\ \Leftrightarrow x = \frac{{\tan {{32}^ \circ }}}{{\tan {{40}^ \circ } - \tan {{32}^ \circ }}}\\ \Leftrightarrow x \approx 2,9\;(km)\end{array}\)
\( \Rightarrow AB \approx \tan {40^ \circ }.2,92 \approx 2,45\;(km)\)
Vậy chiều cao của ngọn núi là 2,45 km.