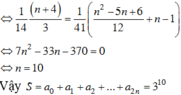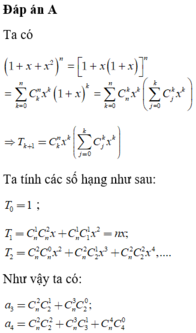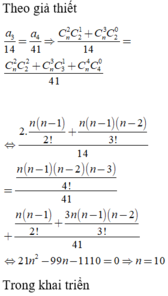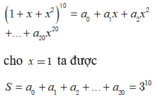Cho f(x)=a0+a1.cosx+a2.cos2x+...+an.cosnxf(x)=a0+a1.cosx+a2.cos2x+...+an.cosnx
biết f(x)>0∀x∈Rf(x)>0∀x∈R
cmr a0>0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 9 2019
Đáp án A
Ta có: 1 + x + x 2 n = 1 + x 1 + x n = ∑ k = 0 n C k n x k 1 + x k
= ∑ k = 0 n C n k x k ∑ j = 0 k C j k x k ⇒ T k + 1 = C k n x k ∑ j = 0 k C j k x k
Ta tính các số hạng như sau:
T 0 = 1 ;
T 1 = C n 1 C n 2 x + C n 1 C 1 1 x 2 = n x ; T 2 = C n 2 C n 0 x 2 + C n 2 C 2 1 x 3 + C n 2 C 2 2 x 4 , ....
Như vậy ta có:
a 3 = C n 2 C 2 1 + C n 3 C 2 0 ; a 4 = C n 2 C 2 2 + C n 3 C 3 1 + C n 4 C 4 0
Theo giả thiết
a 3 14 = a 4 41 ⇒ C n 2 C 2 1 + C n 3 C 2 0 14 = C n 2 C 2 2 + C n 3 C 3 1 + C n 4 C 4 0 41
⇔ 2. n n − 1 2 ! + n n − 1 n − 2 3 ! 14 = n n − 1 2 ! + 3 n n − 1 n − 2 3 ! + n n − 1 n − 2 n − 3 4 ! 41
⇔ 21 n 2 − 99 n − 1110 = 0 ⇒ n = 10
Trong khai triển:
1 + x + x 2 10 = a 0 + a 1 x + a 2 x 2 + ... + a 20 x 20
cho x = 1 ta được: S = a 0 + a 1 + a 2 + ... + a 20 = 3 10