cho tam giác ABC vuông tại A . đường cao AH . trên BC lấy M sao cho CM= CA . đường thẳng qua M song song CA cắt AB tại I .
a )tứ giác ACMI là hình gì . vì sao
b ) chứng minh rằng : 2AH + BC >AB +B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án cần chọn là: C
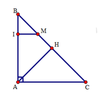
Tứ giác ACMI có: MI //AC (gt) và A ^ = 90 ° (gt) nên là hình thang vuông.

a) Theo đề bài ta có :
\(MI//CA\) ( GT)
=> ACMI là hình thang ( định nghĩa)
Xét hình thang ACMI ta có :
\(\widehat{A}=90^o\)
=> ACMI là hình thang vuông

HÌNH XẤU THÔNG CẢM
a) MI // AC nên \(\widehat{MIA}=\widehat{IAC}=90^o\)
vậy tứ giác ACMI là hình thang vuông
b) CM= CA nên \(\Delta ACM\)cân tại C \(\Rightarrow\widehat{CMA}=\widehat{CAM}\)
Mà \(\widehat{CMA}+\widehat{A_2}=90^o\); \(\widehat{CAM}+\widehat{A_1}=90^o\)
\(\Rightarrow\widehat{A_1}=\widehat{A_2}\)
Xét 2 tam giác vuông : \(\Delta AMH\)và \(\Delta AMI\)có :
\(AM\)chung ; \(\widehat{A_1}=\widehat{A_2}\)( cmt )
\(\Rightarrow\Delta AMH=\Delta AMI\)( cạnh huyền - góc nhọn )
\(\Rightarrow AI=AH\)
c) AB + AC = ( AI + BI ) + CM = AH + CM + BI
Mà \(\Delta BIM\)vuông tại I nên BI < BM
\(\Rightarrow AB+AC=AH+CM+BI< AH+CM+BM=AH+BC\)

a, Vì AC // MI
=> Tứ giác ACMI là hình thang
Vì góc A=90 độ
=> Tứ giác ACMI là hình thang vuông