Trong mặt phẳng tọa độ Oxy , tìm phương trình đường tròn (D') là ảnh của đường tròn (D): (x-1)² +(y+2)²=6 qua T véctơ v với véctơ v =(1;2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 6 2018
a. Phương trình đường tròn : (x – 3)2 + (y + 2)2 = 9.
b. (I1; R1) là ảnh của (I; 3) qua phép tịnh tiến theo vec tơ v.
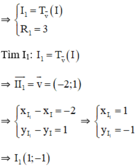
⇒ Phương trình đường tròn cần tìm: (x – 1)2 + ( y + 1)2 = 9.
c. (I2; R2) là ảnh của (I; 3) qua phép đối xứng trục Ox
⇒ R2 = 3 và I2 = ĐOx(I)
Tìm I2: I2 = ĐOx(I) ⇒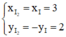 
⇒ I2(3; 2)
⇒ Phương trình đường tròn cần tìm: (x – 3)2 + (y – 2)2 = 9.
d. (I3; R3) là ảnh của (I; 3) qua phép đối xứng qua gốc O.
⇒ R3 = 3 và I3 = ĐO(I)
Tìm I3: I3 = ĐO(I) ⇒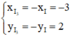 
⇒ Phương trình đường tròn cần tìm: (x + 3)2 +(y – 2)2 = 9.
CM
3 tháng 3 2018
Đáp án B.
Từ C : x + 1 2 + y − 3 2 = 4 có tâm I − 1 ; 3 và bán kính R=2.
V v → I = I ' 2 ; 5 nên có PT là x − 2 2 + y − 5 2 = 4 .
CM
16 tháng 12 2017
Đáp án B.
Từ C : x + 1 2 + y − 3 2 = 4 có tâm I − 1 ; 3 và bán kính R=2 .
V v → I = I ' 2 ; 5 nên có PT là x − 2 2 + y − 5 2 = 4 .
CM
20 tháng 3 2017
Đáp án C
Ta có:
T v → A = A ' ⇒ A A ' = v → ⇔ x A ' - 3 = 1 y A ' - 1 = 2 ⇔ A ' 4 ; - 1
CM
17 tháng 1 2019
Đáp án B
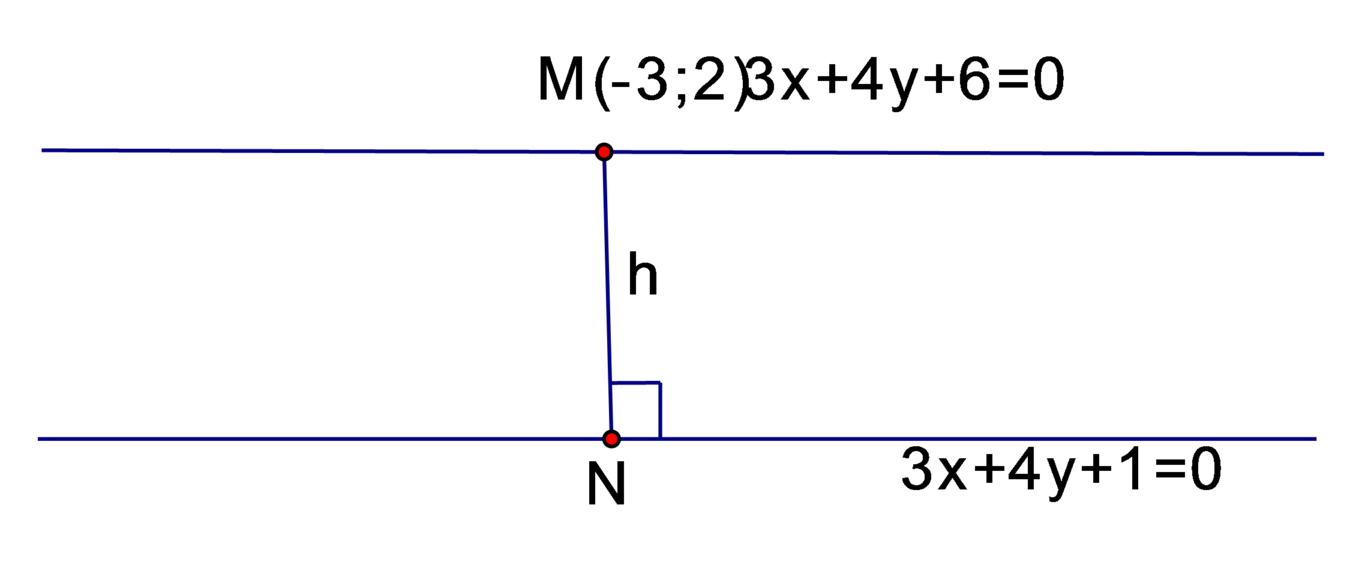
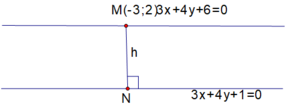
Độ dài véc tơ v → bé nhất đúng bằng khoảng cách h giữa d và d' . h chính là khoảng cách từ M ∈ d tới N ∈ d ' sao cho M N → ⊥ u → 4 ; − 3 trong đó u → là VTCP của cả d và d' .Và khi đó: v → = M N →
Chọn M − 3 ; 2 ∈ d . Ta cần tìm N t ; − 6 − 3 t 4 ∈ d ' sao cho:
M N → t + 3 ; − 14 − 3 t 4 ⊥ u → 4 ; − 3
⇔ 4 t + 12 + 42 + 9 t 4 = 0 ⇔ t = − 18 5
⇒ M N → = − 3 5 ; − 4 5
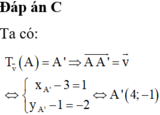
Đường tròn (D) tâm \(I\left(1;-2\right)\) bán kính \(R=\sqrt{6}\)
\(\Rightarrow\) (D') là đường tròn tâm I' là ảnh của I qua phép tịnh tiện \(\overrightarrow{v}\) và bán kính \(R'=R=\sqrt{6}\)
\(\left\{{}\begin{matrix}x'=1+1=2\\y'=-2+2=0\end{matrix}\right.\) \(\Rightarrow I'\left(2;0\right)\)
Phương trình (D'):
\(\left(x-2\right)^2+y^2=6\)