Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
(x + 1)(x + 2)(x + 3)(x + 4) - 24
= x4 + 10x3 + 35x2 + 50x + 24 - 24
= x4 + 10x3 + 35x2 + 50x
( x + 1 ). ( x + 2 ) ( x + 3 ) ( x + 4 ) - 24
= ( x2 + 5x + 4 ) .( x2 + 5x + 6 ) - 24
Đặt t = x2 + 5x + 5
=> ( t - 1 ). ( t + 1 ) - 24
= t2 - 1 - 24
= t2 - 25
= ( t - 5 ). ( t + 5 )
= ( x2 + 5x + 5 - 5 ) . ( x2 + 5x + 5 + 5 )
= ( x2 + 5x ) . ( x2 + 5x + 10 )
= x. ( x + 5 ) . ( x2 + 5x + 10 )
Đặt x^2-3x-2=t =>(t+4)(t-4)+12=t-16+12=t-4=(t+2)(t-2)
=>(x^2-3x-2+2)(x^2-3x-2-2)=(x^2-3x)(x^2-3x-4)
Bạn ơi , mình cho bạn ví dụ và hướng dẫn cách làm nha
f(x)=3x3 – 7x2 + 17x–5f(x)
Hướng dẫn:
±1,±5±1,±5 không là nghiệm của f(x)f(x), như vậy f(x)f(x) không có nghiệm nguyên. Nên f(x)f(x) nếu có nghiệm thì là nghiệm hữu tỉ
Ta nhận thấy x=x= 1313 là nghiệm của f(x)f(x) do đó f(x)f(x) có một nhân tử là 3x–13x–1. Nên
f(x)= 3x3 – 7x2 + 17x – 5 = 3x3− x2− 6x2 + 2x + 15x − 5f(x)
= 3x3 – 7x2 + 17x – 5 = 3x3 − x2 − 6x2 + 2x + 15x − 5
= (3x3−x2 ) − ( 6x2 −2x ) + (15x−5) = (3x3 − x2) − (6x2 − 2x) + (15x−5)
= x2 ( 3x−1 )− 2x(3x−1) + 5(3x−1) = (3x − 1)(x2 − 2x + 5 )
Vì x2 − 2x + 5 = (x2 − 2x + 1) + 4 = (x−1)2 + 4>0x2 − 2x + 5= (x2 − 2x + 1) + 4= (x−1)2 + 4>0 với mọi xx nên không phân tích được thành nhân tử nữa
ình muốn giúp lắm nhưng mình......chưa học.mình mới học lớp 7
Đặt \(x^2+x+1=t\)
Ta có: \(\left(x^2+x+1\right)^2+3x\left(x^2+x+1\right)+2x^2\)
\(=t^2+3xt+2x^2\)
\(=t^2+xt+2xt+2x\)
\(=t\left(t+x\right)+2x\left(t+x\right)\)
\(=\left(t+x\right)\left(t+2x\right)\)
\(=\left(x^2+x+1+x\right)\left(x^2+x+1+2x\right)\)
\(=\left(x^2+2x+1\right)\left(x^2+3x+1\right)\)
\(=\left(x+1\right)^2\left(x^2+3x+1\right)\)
Chúc bạn học tốt.
b)(x2+x+1)(x2+x+2)-12
Đặt t=x2+x+1
t(t+1)-12=t2+t-12
=(t-3)(t+4)=(x2+x+1-3)(x2+x+1+4)
=(x2+x-2)(x2+x+5)
=(x-1)(x+2)(x2+x+5)
c)(x2+8x+7)(x2+8x+15)+15
Đặt t=x2+8x+7
t(t+8)+15=t2+8t+15
=(t+3)(t+5)
=(x2+8x+7+3)(x2+8x+7+15)
=(x2+8x+10)(x2+8x+22)
d)(x+2)(x+3)(x+4)(x+5)-24
=(x2+7x+10)(x2+7x+12)-24
Đặt t=x2+7x+10
t(t+2)-24=(t-4)(t+6)
=(x2+7x+10-4)(x2+7x+10+6)
=(x2+7x+6)(x2+7x+16)
=(x+1)(x+6)(x2+7x+16)
a/ Đặt x2 + 4x + 8 = a
Thì đa thức ban đầu thành
a2 + 3ax + 2x2 = (a2 + 2ax + x2) + (ax + x2)
= (a + x)2 + x(a + x) = (a + x)(a + 2x)
a)x4+2x3+5x2+4x-12
=(x4+2x3+x2)+(4x2+4x)-12
=(x2+x)2+4(x2+x)-12
Đặt t=x2+x
=t2+4t-12=(t-2)(t+6)
=(x2+x-2)(x2+x+6)
=(x-1)(x+2)(x2+x+6)
b)(x+1)(x+2)(x+3)(x+4)+1
=(x2+5x+4)(x2+5x+6)+1
Đặt x2+5x+4=t
t(t+2)+1=t2+2t+1
=(t+1)2=(x2+5x+4+1)2
=(x2+5x+5)2
c)(x+1)(x+3)(x+5)(x+7)+15
=(x2+8x+7)(x2+8x+15)+15
Đặt t=x2+8x+7
t(t+8)+15=(t+3)(t+5)
=(x2+8x+7+3)(x2+8x+7+5)
=(x2+8x+10)(x+2)(x+6)
d)(x+1)(x+2)(x+3)(x+4)-24
=(x2+5x+4)(x2+5x+6)-24
Đặt t=x2+5x+4
t(t+2)-24=(t-4)(t+6)
=(x2+5x+4-4)(x2+5x+4+6)
=x(x+5)(x2+5x+10)
Đặt x^2+2x=t =>3t^2-2t-1=3t^2-3t+t-1=3t(t-1)+(t-1)=(t-1)(3t+1)
=>(x^2+2x-1)(3x^2+6x+1)
Bạn nên tách bài ra để đăng. Không nên đăng 1 loạt như thế này.
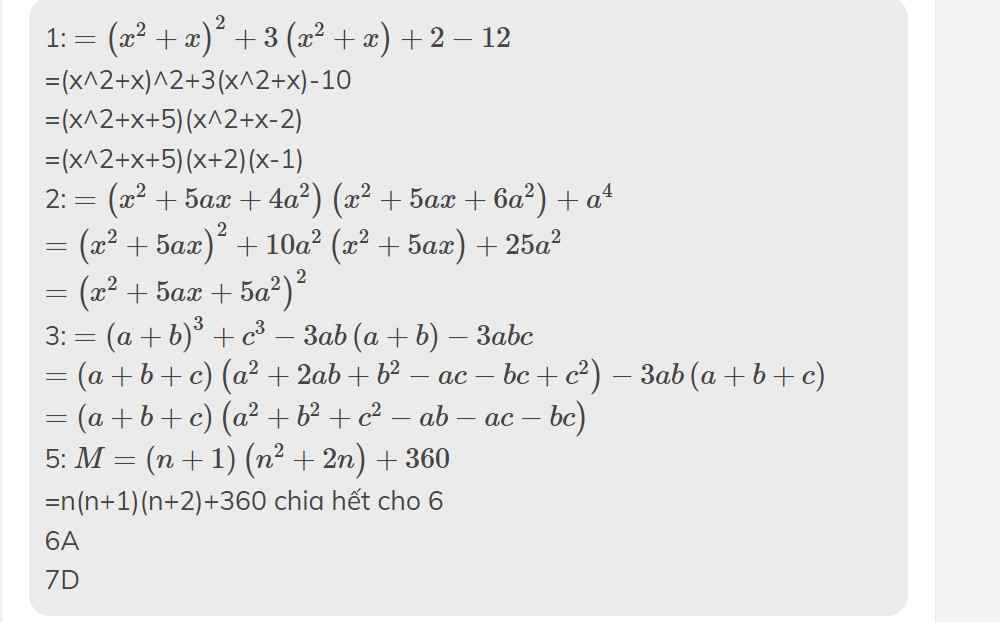
a. (x2 + x)2 + 4.(x2 + x) - 12 (*)
Đặt x2 + x = a, ta có:
(*) = a2 + 4a - 12
= (a2 + 4a + 4) - 16
= (a + 2)2 - 16
= (a + 6)(a - 2)
= (x2 + x + 6)(x2 + x - 2)
b. (x2 + x+ 1)(x2 + x + 2) - 12 (**)
Đặt x2 + x + 1 = t, ta có:
(**) = t.(t + 1) - 12
= t2 + t - 12
= t2 + 4t - 3t - 12
= t(t + 4) - 3(t + 4)
= (t - 3)(t + 4)
= (x2 + x - 2)(x2 + x + 5)
c. (x + 1)(x + 2)(x + 3)(x + 4) - 24 (***)
= (x2 + 5x + 4)(x2 + 5x + 6) - 24
Đặt x2 + 5x + 4 = k, ta có:
(***) = k.(k + 2) - 24
= k2 + 2x - 24
= k2 + 6k - 4k - 24
= k(k + 6) - 4(k + 6)
= (k - 4)(k + 6)
= (x2 + 5x)(x2 + 5x + 10)