Cho \(\dfrac{a}{b}\)=\(\dfrac{c}{d}\). CMR : \(\dfrac{a.c}{b.d}\)=\(\dfrac{a^2+c^2}{b^2+d^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 10 2021
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\Rightarrow\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{b^2k^2+d^2k^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\\ \dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=k^2\\ \Rightarrow\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{ac}{bd}\)
26 tháng 8 2021
Đề sai rồi bạn. Phải thay "^2" bằng "^3" mới đúng.
19 tháng 2 2021
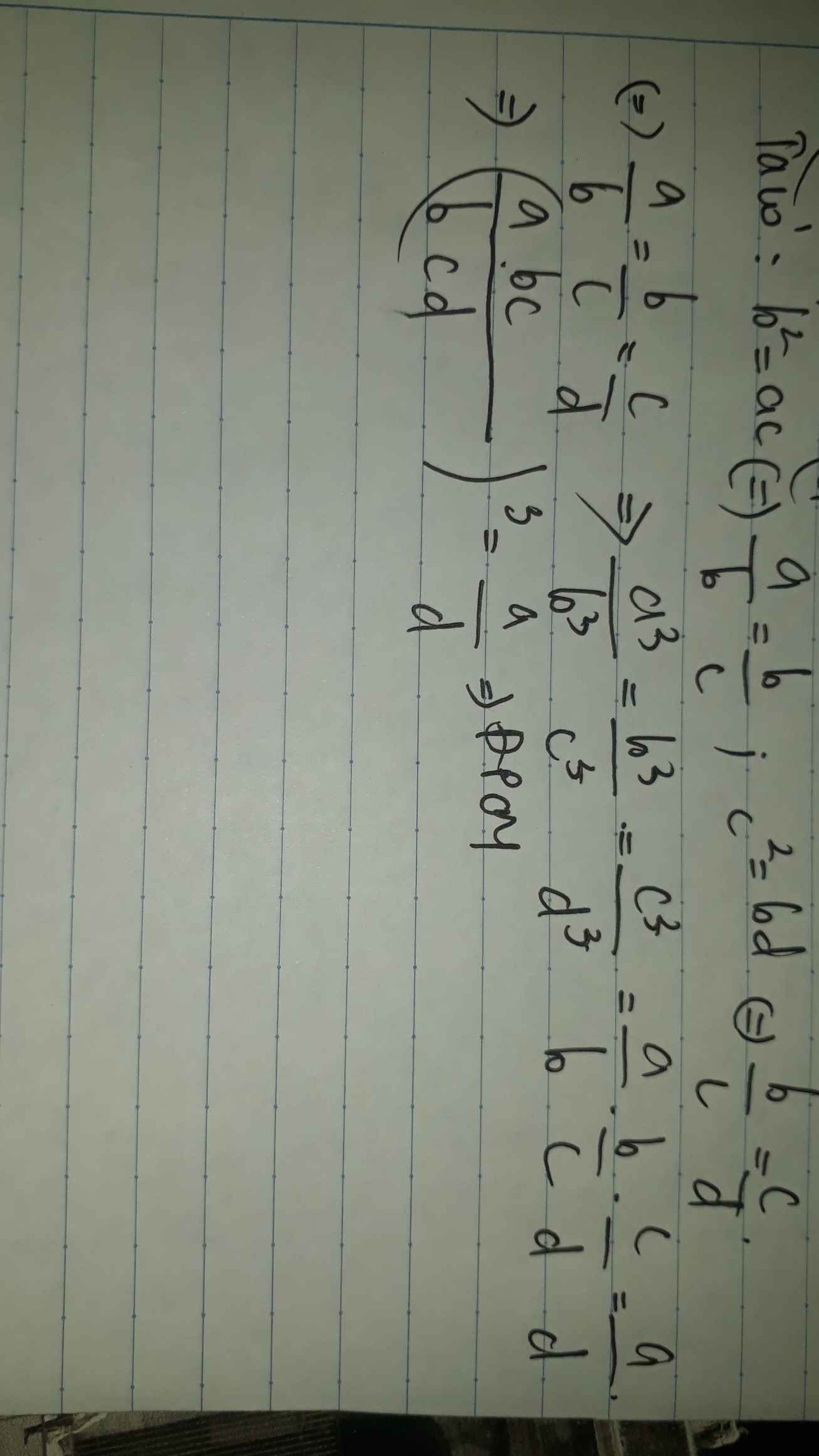
a) Ta có: \(\dfrac{a}{b}=\dfrac{c}{d}\)
\(\Leftrightarrow\dfrac{b}{a}=\dfrac{d}{c}\)
\(\Leftrightarrow\dfrac{b}{a}-1=\dfrac{d}{c}-1\)
\(\Leftrightarrow\dfrac{b-a}{a}=\dfrac{d-c}{c}\)
\(\Leftrightarrow\dfrac{a-b}{a}=\dfrac{c-d}{c}\)
\(\Leftrightarrow\dfrac{a}{a-b}=\dfrac{c}{c-d}\)(đpcm)
LV
3
19 tháng 8 2017
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
=>\(a=bk\),\(c=dk\)
\(\dfrac{a^2}{b^2}=\dfrac{bk^2}{b^2}=k^2\left(1\right)\)
\(\dfrac{ac}{bd}=\dfrac{bk.dk}{bd}=k^2\left(2\right)\)
Từ (1) và (2)=>\(\dfrac{a^2}{b^2}=\dfrac{ac}{bd}\)(đpcm)
EJ
19 tháng 8 2017
Đặt \(\dfrac{a}{b}=k;\dfrac{c}{d}=k\)
\(\Rightarrow a=kb;c=kd\)
\(\Rightarrow\dfrac{a^2}{b^2}=\dfrac{bk^2}{b^2}=k^2\)
\(\Rightarrow\dfrac{ac}{bd}=\dfrac{bkdk}{bd}=k^2\)
Từ các chứng minh trên cho ta thấy
\(\Rightarrow\dfrac{a^2}{b^2}=\dfrac{a.c}{b.d}\)
HN
29 tháng 3 2017
Ta có:
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}=\dfrac{a-c}{b-d}=\dfrac{3a}{3b}=\dfrac{2c}{2d}=\dfrac{3a-2c}{3b-2d}\)
a/ \(\dfrac{a.c}{b.d}=\dfrac{\left(a+c\right).\left(a-c\right)}{\left(b+d\right).\left(b-d\right)}=\dfrac{a^2-c^2}{b^2-d^2}\)
b/ \(\dfrac{a^2}{b^2}=\dfrac{a}{b}.\dfrac{3a-2c}{3b-2d}=\dfrac{3a^2-2ac}{3b^2-2bd}\)
16 tháng 3 2023
\(\left.\begin{matrix} b^2=ac\Rightarrow \dfrac{a}{b}=\dfrac{b}{c} \\c^2=bd \Rightarrow \dfrac{b}{c}=\dfrac{c}{d}\end{matrix}\right\}\)
\(\Rightarrow\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}\\ \Rightarrow\dfrac{a^3}{b^3}=\dfrac{b^3}{c^3}=\dfrac{c^3}{d^3}\)
Áp dụng t/c của DTSBN , ta có :
\(\dfrac{a^3}{b^3}=\dfrac{b^3}{c^3}=\dfrac{c^3}{d^3}=\dfrac{a^3+b^3+c^3}{b^3+c^3+d^3}\\ \Rightarrow\dfrac{a^3}{b^3}=\dfrac{a^3+b^3+c^3}{d^3+c^3+d^3}\left(1\right)\)
Có `a^3/b^3=a/b*a/b*a/b=a/b*b/c*c/d=a/d` ( do `a/b=b/c=c/d` )`(2)
Từ `(1);(2)=>` \(\dfrac{a}{d}=\dfrac{a^3+b^3+c^3}{b^3+c^3+d^3}\)
TN
cho \(b^2=a.c-a^2=b.d\)
c/m:\(\dfrac{a^3+b^3-c^3}{b^3+c^2-d^3}=\left(\dfrac{a+b-c}{b+c-d}\right)^2\)
2
23 tháng 10 2018
\(b^2=a.c\)
\(\Rightarrow\dfrac{a}{b}=\dfrac{b}{c}\left(1\right)\)
\(c^2=b.d\)
\(\Rightarrow\dfrac{b}{c}=\dfrac{c}{d}\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{a+b-c}{b+c-d}\)
\(\Rightarrow\left(\dfrac{a}{b}\right)^3=\left(\dfrac{b}{c}\right)^3=\left(\dfrac{c}{d}\right)^3=\left(\dfrac{a+b-c}{b+c-d}\right)^3\)
\(=\dfrac{a^3}{b^3}=\dfrac{b^3}{c^3}=\dfrac{c^3}{d^3}=\left(\dfrac{a+b-c}{b+c-d}\right)^3=\dfrac{a^3+b^3-c^3}{b^3+c^3-d^3}\left(đpcm\right)\)
Đặt :
\(\dfrac{a}{b}=\dfrac{c}{d}=k\) \(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
\(VT=\dfrac{ac}{bd}=\dfrac{bk.dk}{bd}=\dfrac{bd.k^2}{bd}=k^2\left(1\right)\)
\(VP=\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\dfrac{b^2.k^2+d^2.k^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\left(2\right)\)
Từ \(\left(1\right)+\left(2\right)\Leftrightarrow\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}\left(đpcm\right)\)