tính khoảng cách d giữa hai diểm cực tiểu của đồ thị hàm số y= x^4-4x^2+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
5 tháng 1 2017
Đáp án C.
y = (x + 1)(x – 2)2.
y' = 3x2 – 6x
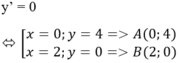
Khoảng cách giữa hai điểm cực trị AB = 2√5

CM
15 tháng 3 2018
Ta có
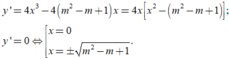
Suy ra đồ thị có hai điểm cực tiểu là A - m 2 - m + 1 ; y C T và B m 2 - m + 1 ; y C T
Khi đó 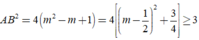
Dấu xảy ra khi m=1/2.
Chọn B.

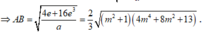

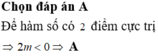

Lời giải:
\(y=x^4-4x^2+1\Rightarrow y'=4x^3-8x=0\)
\(\Leftrightarrow \left[\begin{matrix} x=0\\ x=\pm \sqrt{2}\end{matrix}\right.\)
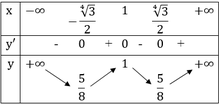
Lập bảng biến thiên, ta thấy $y$ đạt cực tiểu tại \(x=\sqrt{2}; -\sqrt{2}\), tương ứng với $y=-3$
Do đó, khoảng cách d giữa 2 điểm cực tiểu của đths là:
\(d=\sqrt{(\sqrt{2}--\sqrt{2})^2+(-3--3)^2}=2\sqrt{2}\)