tìm X biết tanX + cotX=2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Chọn B.
Ta có: A = (tanx + cotx)2 - ( tanx - cotx)2
= tan2x + 2tanx.cot x + cot2x - ( tan2x - 2tanx.cotx + cot2x)
= 4tanx.cotx = 4.


a) Hàm số y = tanx nhận giá trị bằng – 1
- Vẽ hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = - 1
- Lấy giao điểm của hai hàm số y = tanx và y = - 1
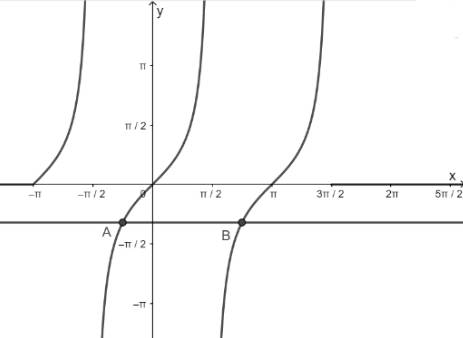
b) Hàm số y = tanx nhận giá trị bằng 0
- Vẽ hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = tanx và y = 0
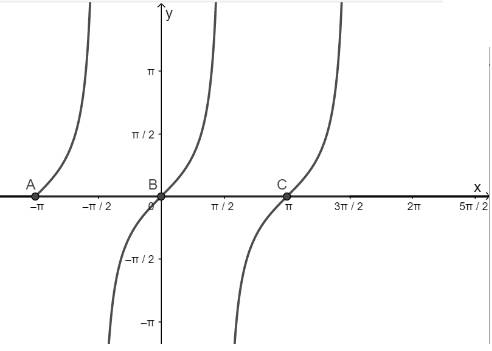
c) Hàm số y = cotx nhận giá trị bằng 1
- Vẽ hàm số y = cotx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 1
- Lấy giao điểm của hai hàm số y = cotx và y = 1
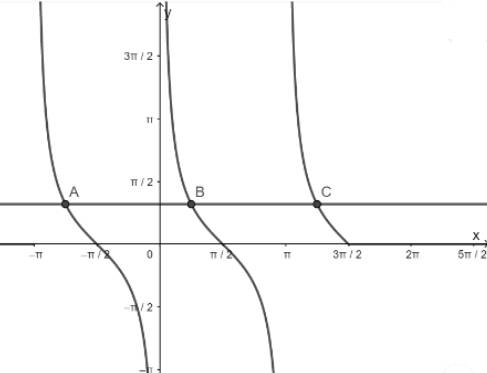
d) Hàm số y = cotx nhận giá trị bằng 0
- Vẽ hàm số y = cotx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = tanx và y = 0
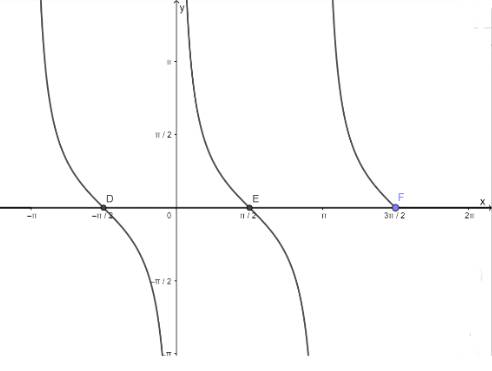

a: pi<x<3/2pi
=>sinx<0 và cosx<0
\(1+tan^2x=\dfrac{1}{cos^2x}\)
=>\(\dfrac{1}{cos^2x}=1+\dfrac{9}{4}=\dfrac{13}{4}\)
=>\(cos^2x=\dfrac{4}{13}\)
=>\(\left\{{}\begin{matrix}cosx=-\dfrac{2}{\sqrt{13}}\\sin^2x=\dfrac{9}{13}\end{matrix}\right.\)
mà sin x<0
nên \(sinx=-\dfrac{3}{\sqrt{13}}\)
\(cotx=1:\dfrac{3}{2}=\dfrac{2}{3}\)
b: 0<x<90 độ
=>sin x>0 và cosx>0
\(1+tan^2x=\dfrac{1}{cos^2x}\)
=>\(\dfrac{1}{cos^2x}=1+\dfrac{1}{3}=\dfrac{4}{3}\)
=>\(cos^2x=\dfrac{3}{4}\)
=>\(cosx=\dfrac{\sqrt{3}}{2}\)
=>\(sinx=\dfrac{1}{2}\)
cotx=1:căn 3/3=3/căn 3=căn 3
c: 3/2pi<x<2pi
=>sinx<0 và cosx>0
\(1+cot^2x=\dfrac{1}{sin^2x}\)
=>\(\dfrac{1}{sin^2x}=1+\dfrac{1}{3}=\dfrac{4}{3}\)
=>\(sin^2x=\dfrac{3}{4}\)
mà sin x<0
nên \(sinx=-\dfrac{\sqrt{3}}{2}\)
\(cos^2x=1-\dfrac{3}{4}=\dfrac{1}{4}\)
mà cosx>0
nên cosx=1/2
x=450
tanX +cotX = 2
<=> tanX +cotX -2=0
<=> tanX + \(\dfrac{1}{tanX}\) -2 =0
<=> \(\dfrac{\text{tan^2 X + 1 - 2tanX}}{tanX}\)=0
=> tan2X +1 - 2tanX=0
Đặt tanX=t
=> t2 -2t +1=0
<=> (t-1)2=0
=> t=1 <=> tanX=1=> x=45o
Vậy x=45o