Đặt một vật sáng AB trước thấu kính hội tụ sao cho A nằm trên trục chính và AB nghiêng với trục chính một góc \(60^0\) . Biết \(OA=40cm\) , \(AB=8cm\) , \(f=20cm\) .
a ) Hãy dựng ảnh của vật AB qua thấu kính ( câu này mình làm được rồi )
b ) Xác định độ lớn của ảnh . ( Tính đoạn \(A'B'\) )
Nguyễn Hải Dương nguyen thi vang Tenten
...
Đọc tiếp
Đặt một vật sáng AB trước thấu kính hội tụ sao cho A nằm trên trục chính và AB nghiêng với trục chính một góc \(60^0\) . Biết \(OA=40cm\) , \(AB=8cm\) , \(f=20cm\) .
a ) Hãy dựng ảnh của vật AB qua thấu kính ( câu này mình làm được rồi )
b ) Xác định độ lớn của ảnh . ( Tính đoạn \(A'B'\) )
Nguyễn Hải Dương nguyen thi vang Tenten
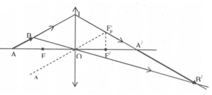
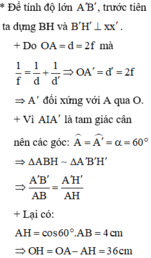
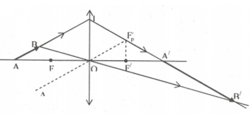
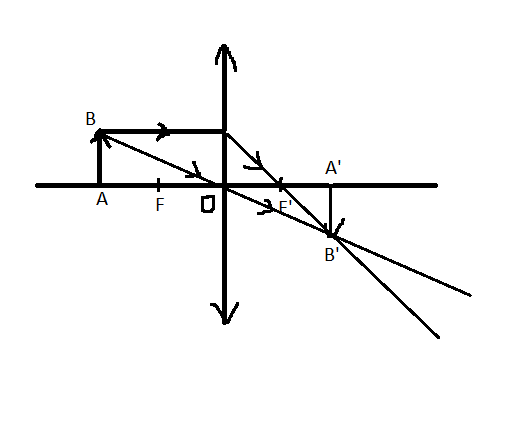
Bạn vẽ BH vuông góc với trục chính
B'H' là ảnh thật của BH qua thấu kính
Bạn tự chứng minh công thức \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\)(*)( đối với thấu kính hội tụ cho ảnh thật nhé )
Sử dụng hệ thức lượng vào tam giác ABH
cos60=\(\dfrac{AH}{AB}=\dfrac{1}{2}=>AH=2\)cm=>HO=AO-AH=38cm
sử dụng công thức (*) vì B'H' là ảnh thật =>\(\dfrac{1}{f}=\dfrac{1}{HO}+\dfrac{1}{H'O}\)=>H'0=\(\dfrac{380}{9}cm\)
Tương tự ta cũng tính được OA'=40cm ( với công thức * ; OA=40cm và f=20cm)
Vì OA'=OA => \(\Delta AIA'\) cân có OI trung tuyến + đường cao
=> Góc IAO=góc IA'O=60 độ=>góc B'A'H' = 60 độ ( đối đỉnh)
Sử dụng hệ thức lượng vào \(\Delta B'A'H'\) ta có cos60=\(\dfrac{A'H'}{A'B'}=\dfrac{OH'-OA'}{A'B'}=\dfrac{1}{2}=>A'B'=\dfrac{40}{9}cm\)
Bạn post hình vẽ lên để Ten làm cho, Ten nhác vẽ lắm !