Cho hàm số y = x2 có đồ thị ( P ) và hàm số y = 4x + m có đồ thị ( dm ) . Tìm tất cả các giá trị của m sao cho ( dm ) và ( P ) cắt nhau tại 2 điểm phân biệt , trong đó tung độ của một trong hai giao điểm đó bằng 1 .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 6 2015
1, bạn tự vẽ nha
2, xét pt: \(x^2=4x+m\Leftrightarrow x^2-4x-m=0\)(1) ; \(\Delta=16-4.-m=16+16m\)
(dm) và (P) cắt nhau tại hai điểm phân biệt <=> pt có 2 nghiệm p.biệt <=> \(\Delta>0\Leftrightarrow16+16m>0\Leftrightarrow m>-1\)
th1: chọn tung độ của giao điểm 1 là 1 <=> y1=1<=> \(x1=\sqrt{y1}=\sqrt{1}=1\); \(x1=\frac{4+\sqrt{16\left(m+1\right)}}{2}=\frac{4\left(1+\sqrt{m+1}\right)}{2}=2+2\sqrt{m+1}\)
thay x=1 vào ta có: \(2+2\sqrt{m+1}=1\Leftrightarrow2\sqrt{m+1}=-1\Rightarrow\)PTVN
th2: y2=1 <=> x2=1
\(x2=\frac{4-\sqrt{16\left(m+1\right)}}{2}=2-2\sqrt{m+1}\). thay x2=1 vào: \(2-2\sqrt{m+1}=1\Leftrightarrow-2\sqrt{m+1}=-1\Leftrightarrow\sqrt{m+1}=\frac{1}{2}\Leftrightarrow m+1=\frac{1}{4}\Leftrightarrow m=-\frac{3}{4}\)(t/m đk)
=> m=-3/4 thì (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó tung độ của một trong hai giao điểm đó bằng 1.
17 tháng 6 2017
xset pt tg giao đc đk của m là m > -4
áp dụng viet ;
x1 .x2 = -m
x1 + x2 =4
vì tọa độ cát có tung độ là 1 suy ra x1 hoắc x2 =1 thế vào viet tìm m = -3 ( tm m > -4 )suy ra m =-3 thf cắt tại 2 điểm pb trong đó....
10 tháng 8 2019
1.
để ............. căt nhau tại 1 điểm trên trục tung thì:
\(\hept{\begin{cases}0\ne2\left(T.m\right)\\2+m=3-m\end{cases}}\)
<=>2m=1
<=>m=1/2
15 tháng 4 2021
a) Phương trình hoành độ giao điểm là:
\(x^2=2x-m+2\)
\(\Leftrightarrow x^2-2x+m-2=0\)
Để hai đồ thị hàm số chỉ có một điểm chung thì Δ=0
\(\Leftrightarrow4-1\cdot\left(m-2\right)=0\)
\(\Leftrightarrow m-2=4\)
hay m=6
CM
13 tháng 1 2018
Phưng trình hoành độ giao điểm:
Đường thẳng d cắt đồ thị (C) tại 2 điểm phân biệt
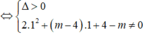
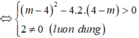
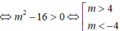
Khi đó, (*) có hai nghiệm phân biệt x 1 ; x 2 thỏa mãn:
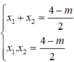
Tọa độ hai giao điểm là:
= 5 . x 1 - x 2 2
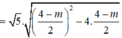
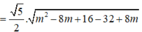
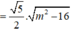
Giao điểm của hai đường tiệm cận của đồ thị (C) là: I(1;2)
Ta có: 
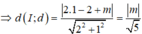
Ta có:
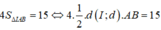
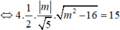
(thỏa mãn)
Chọn đáp án A.
CM
20 tháng 8 2019
Đáp án C
Phương trình hoành độ giao điểm là: m x 3 - x 2 2 x + 8 m = 0
⇔ m x + 2 x 2 - 2 x + 4 - x x + 2 = 0 ⇔ x + 2 m x 2 - 2 m x + 4 m - x = 0 ⇔ [ x = - 2 g x = m x 2 - 1 + 2 m x + 4 m = 0
Để đồ thị C m cắt trục hoành tại ba điểm phân biệt thì g x = 0 có 2 nghiệm phân biệt khác -2 ⇔ m ≠ 0 ∆ = 1 + 2 m 2 - 16 m 2 > 0 g - 2 = 4 m + 2 1 + 2 m + 4 m ≠ 0 ⇔ m ∈ - 1 6 ; 1 2 \ 0
Thay y=1 vào (P), ta được:
\(x^2=1\)
=>x=1 hoặc x=-1
Thay x=1 và y=1 vào y=4x+m, ta được:
m+4=1
hay m=-3
Thay x=-1 và y=1 vào y=4x+m, ta được:
m-4=1
hay m=5