trên cùng một hệ trục tọa độ
a. vẽ đồ thị (P) hàm số y=\(\dfrac{x^2}{2}\)
b. trên (P) lấy hai điểm A và B có hoành độ bằng 1 và -2. viết phương trình đường thẳng đi qua hai điểm A và B
c. từ gốc tọa độ O ta vẽ đường thẳng (d) song song với AB. tìm tọa độ giao điểm của (P) và đường thẳng (d) bằng phương pháp đại số

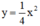
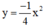
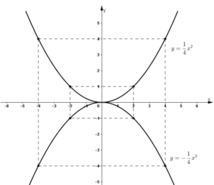
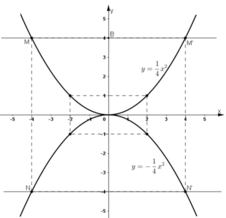
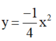 tại N và N’.
tại N và N’.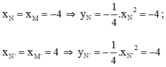
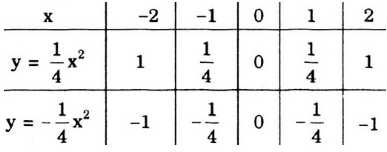
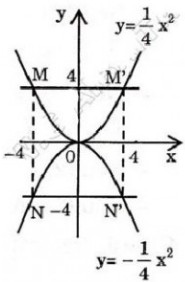

a. Tự vẽ nha.
b. Gọi A(x0;y0) và B(x1;y1).
Thay x0=1;x1=-2 vào (P), ta được:
y0=\(\dfrac{1}{2};y_1=\dfrac{4}{2}=2\)
Gọi a: ax+b đi qua A và B. Ta có hpt:
\(\left\{{}\begin{matrix}a+b=\dfrac{1}{2}\\-2a+b=2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{-1}{2}\\b=1\end{matrix}\right.\)
Vậy a: \(\dfrac{-1}{2}x+1\) đi qua A và B.
c) Có (d) đi qua O và // (P) nên ta có: d: a'x+b' có a'=\(a=\dfrac{-1}{2}\); b'\(\ne b\ne1\)
Thay x=0; y=0 vào (d), ta có: 0+b'=0=>b'=0.
Vậy d: \(y=\dfrac{-1}{2}x\)
Gọi D,E là giao của (P) và (d). Ta có pt hoành độ giao điểm:
\(\dfrac{x^2}{2}=\dfrac{-1}{2}x\)
\(\Rightarrow x^2+x=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}y=0\\y=\dfrac{1}{2}\end{matrix}\right.\)
Vậy (P) giao với (d) tại 2 điểm D(0;0) và E\(\left(-1;\dfrac{1}{2}\right)\).