vt chương trình tính
S=\(\dfrac{2}{1}+\dfrac{3}{2}+\dfrac{4}{3}+.........+\dfrac{n+1}{n}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

#include <bits/stdc++.h>
using namespace std;
double s,a;
int i,n;
int main()
{
cin>>a;
s=0;
n=0;
while (s<=a)
{
n=n+1;
s=s+1/(n*1.0);
}
cout<<n;
return 0;
}

Bài 1:
uses crt;
var n,i:integer;
s:real;
begin
clrscr;
write('Nhap n='); readln(n);
s:=0;
for i:=1 to n do
s:=s+1/(2*i+1);
writeln(s:4:2);
readln;
end.

Program HOC24;
var s: real;
i,n: integer;
function tong(x: integer): longint;
var j: integer;
t: longint;
begin
t:=0;
for j:=1 to x do t:=t+j;
tong:=t;
end;
function tich(s: integer): longint;
var j1: integer;
t1: longint;
begin
t1:=1;
for j1:=1 to s do t1:=t1*j1;
tich:=t1;
end;
begin
write('Nhap N : '); readln(n);
for i:=1 to n do s:=s+tong(i)/tich(i);
write('S = ',S:2:2);
readln
end.
uses crt;
var s:real;
i,n:longint;
{------------ham-tinh-giai-thua------------------------}
function gthua(x:longint):real;
var gt:real;
i:longint;
begin
gt:=1;
for i:=1 to x do
gt:=gt*i;
gthua:=gt;
end;
{-------------------chuong-trinh-con-tinh-tong---------------------}
function tong(x:longint):real;
var t:real;
i:longint;
begin
t:=0;
for i:=1 to x do
t:=t+i;
tong:=t;
end;
{------------------chuong-trinh-chinh--------------------}
begin
clrscr;
write('Nhap n='); readln(n);
s:=0;
for i:=1 to n do
s:=s+(tong(i)/gthua(i));
writeln('Ket qua la: ',s:4:2);
readln;
end.

a: \(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{10}-\dfrac{3}{202}=\dfrac{150}{101}\)
b: 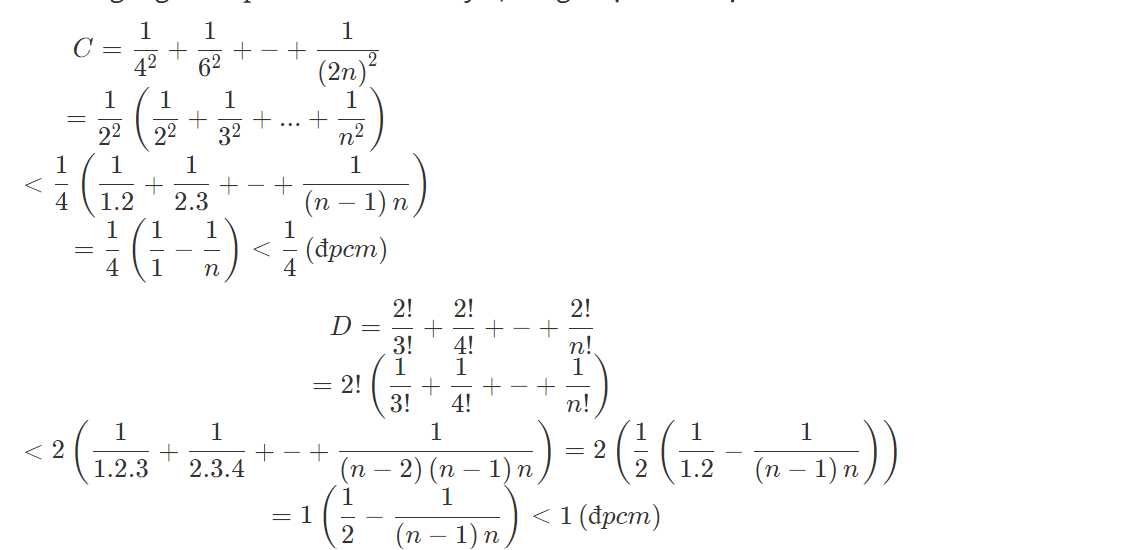

program Bai_1;
uses crt;
var n,i:integer; s:real;
begin
clrscr;
write('Nhap n: '); readln(n);
for i:=1 to n do s:=s+1/(2*i);
write('S=',s);
readln;
end.
program Bai_2;
uses crt;
var n,i:integer; gt:longint; s:real;
begin
clrscr;
write('n='); readln(n);
gt:=1;
for i:=1 to n do
begin
gt:=gt*i;
s:=s+1/gt;
end;
write('S=',s);
readln;
end.
- nếu như khai báo biến S:real thì nên thêm độ rộng chữ số vào kq

1:
\(S=-\left(1-\dfrac{1}{10}+\dfrac{1}{10^2}-...-\dfrac{1}{10^{n-1}}\right)\)
\(=-\left[\left(-\dfrac{1}{10}\right)^0+\left(-\dfrac{1}{10}\right)^1+...+\left(-\dfrac{1}{10}\right)^{n-1}\right]\)
\(u_1=\left(-\dfrac{1}{10}\right)^0;q=-\dfrac{1}{10}\)
\(\left(-\dfrac{1}{10}\right)^0+\left(-\dfrac{1}{10}\right)^1+...+\left(-\dfrac{1}{10}\right)^{n-1}\)
\(=\dfrac{\left(-\dfrac{1}{10}\right)^0\left(1-\left(-\dfrac{1}{10}\right)^{n-1}\right)}{-\dfrac{1}{10}-1}\)
\(=\dfrac{1-\left(-\dfrac{1}{10}\right)^{n-1}}{-\dfrac{11}{10}}\)
=>\(S=\dfrac{1-\left(-\dfrac{1}{10}\right)^{n-1}}{\dfrac{11}{10}}\)
2:
\(S=\left(\dfrac{1}{3}\right)^0+\left(\dfrac{1}{3}\right)^1+...+\left(\dfrac{1}{3}\right)^{n-1}\)
\(u_1=1;q=\dfrac{1}{3}\)
\(S_{n-1}=\dfrac{1\cdot\left(1-\left(\dfrac{1}{3}\right)^{n-1}\right)}{1-\dfrac{1}{3}}\)
\(=\dfrac{3}{2}\left(1-\left(\dfrac{1}{3}\right)^{n-1}\right)\)
\(1,\) Ta có \(\left\{{}\begin{matrix}q=\dfrac{u_2}{u_1}=\dfrac{1}{10}:\left(-1\right)=-\dfrac{1}{10}\\u_1=-1\end{matrix}\right.\)
Vậy \(S=-1+\dfrac{1}{10}-\dfrac{1}{10^2}+...+\dfrac{\left(-1\right)^n}{10^{n-1}}=\dfrac{-1}{1-\left(-\dfrac{1}{10}\right)}=-\dfrac{10}{11}\)
\(2,\) Ta có \(\left\{{}\begin{matrix}q=\dfrac{u_2}{u_1}=\dfrac{1}{3}\\u_1=1\end{matrix}\right.\)
Vậy \(S=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{n-1}}=\dfrac{1}{1-\dfrac{1}{3}}=\dfrac{3}{2}\)
Uses crt;
Var i,n:integer;
S:real;
Begin
Clrscr;
Write('Nhap n = ');Readln(n);
S:=0;
For i:=1 to n do
S:=S+(i+1)/2;
Write(S:0:1);
Readln
End.
{ Có sai sót gì thì cho mình xin lỗi, phần S có thể ra số vô tỉ nên mình làm tròn số lại =) }