cho Hthang ABCD (AB//CD) có AB+CD=15,BD=9 , AC=12. TÍNH diện tích của thang
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:

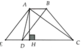
Kẻ đường cao $AE$ và $BF$ của hình thang. Ký hiệu \(DE=a, EF=b, FC=c\)
Có \(\widehat{EAB}=180^0-\widehat{AEF}=180^0-90^0=90^0\). Như vậy tứ giác $ABFE$ có ba góc vuông nên là hình chữ nhật
\(\Rightarrow AB=EF=b\)
\(\Rightarrow AB+CD=2b+a+c=15\)
Áp dụng định lý Pitago cho các tam giác vuông:
\(AE^2+EC^2=AC^2\Leftrightarrow AE^2+(b+c)^2=144(1)\)
\(BF^2+DF^2=BD^2\Leftrightarrow BF^2+(a+b)^2=81(2)\)
Lấy \((1)-(2)\Rightarrow (b+c-a-b)(a+2b+c)=63\) (do \(AE=BF\) )
\(\Leftrightarrow (c-a).15=63\Rightarrow c-a=4,2\)
\(\Rightarrow 15=a+2b+c=a+2b+a+4,2\)
\(\Rightarrow b+a=5,4\)
Thay vào (2) suy ra: \(BF^2=\frac{1296}{25}\Rightarrow BF=7,2\)
\(S_{ABCD}=\frac{(AB+CD).BF}{2}=\frac{15.7,2}{2}=54\)

Qua A kẻ AE//BD (E Î DC)
Þ AE = BD = 12cm, DE = AB = 5cm
Þ DAEC vuông tại A (định lý Pytago đảo)
⇒ A H = A E . A C E C = 12.16 20 = 9 , 6 c m
Þ SABCD = 96cm2

kẻ 1 đường thẳng // với 1 đường chéo rồi chứng mình tam giác vuông
Thầy Vũ Tiền Châu , thầy giải thích rõ tí đc k ạ ? E vẽ thử mà nghĩ hoài k ra
