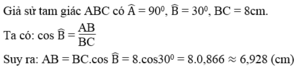Cho tam giác ABC.có góc A = \(90^o\), AB = 5, BC = 7 .Hãy giải tam giác ABC (làm tròn đến chữ số thập phân thứ ba)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 7 2021
Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan25^0\)
\(\Leftrightarrow AC=8\cdot\tan25^0\)
hay \(AC\simeq3,730\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=8^2+3.73^2=77,9129\)
hay \(BC\simeq8,827\left(cm\right)\)
CM
14 tháng 4 2017
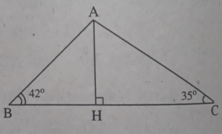
Đặt AH = h thì rõ ràng BH = h.cotg (ABH) = h. cotg 42 °
CH = h.cotg (ACH) = h.cotg 35 ° (để ý rằng H thuộc đoạn BC vì 35 ° , 42 ° đều là góc nhọn).
Do đó: 7 = BC = BH + CH = h(cotg 42 ° + cotg 35 ° ), suy ra
8 tháng 11 2021
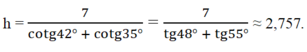
\(AB=\cos B\cdot BC=\dfrac{1}{2}\cdot20=10\left(cm\right)\\ AC=\sin B\cdot BC=\dfrac{\sqrt{3}}{2}\cdot20=10\sqrt{3}\approx17,3205\left(cm\right)\\ \widehat{C}=90^0-\widehat{B}=30^0\)
14 tháng 6 2023
AC=căn 7^2-5^2=2căn6(cm)
sin C=5/7
=>góc C=45 độ 35'
=>góc B=44 độ 25'
S
4 tháng 6 2021
Bạn ơi ! Thiếu dữ kiện rồi !
Tam giác thường có 2 cạnh mà không cho thêm gì thì hơi khó à nha
11 tháng 12 2023
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{3}{5}\)
nên \(\widehat{B}\simeq36^052'\)
Ta có: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{C}=90^0-36^052'=53^08'\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot7,5=4,5\cdot6=27\)
=>AH=27/7,5=3,6(cm)