Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
A)VÌ AD LÀ TRUNG TUYẾN CỦA \(\Delta ABC\)
MÀ G LÀ TRỌNG TÂM CỦA \(\Delta ABC\)
\(\Rightarrow AG=2GD\)
MÀ \(AG=GM\)( G LÀ TRUNG ĐIỂM CỦA AM )
\(\Rightarrow GM=2GD\)
NÊN D LÀ TRUNG ĐIỂM CỦA GM
\(\Rightarrow GD=DM\left(ĐPCM\right)\)
XÉT \(\Delta BDM\)VÀ\(\Delta CDG\)CÓ
\(BD=CD\left(GT\right)\)
\(\widehat{BDM}=\widehat{CDG}\)( ĐỐI ĐỈNH)
\(GD=DM\left(CMT\right)\)
=>\(\Delta BDM\)=\(\Delta CDG\)( C-G-C)
B)
VÌ CE LÀ TRUNG TUYẾN CỦA \(\Delta ABC\)
MÀ G LÀ TRỌNG TÂM CỦA \(\Delta ABC\)
\(\Rightarrow CG=\frac{2}{3}CE\)
THAY\(CG=\frac{2}{3}.6=4\left(CM\right)\)
MÀ \(\Delta BDM\)=\(\Delta CDG\)( CMT)
=>\(BM=CG=4\left(CM\right)\)
C)
TA CÓ
\(AB< DB+DA\)
\(AC< DC+DA\)
CỘnG VẾ THEO VẾ
\(\Rightarrow AB+AC< 2AD+DB+DC\)
GIẢI TIẾP LÀ RA
Gọi I, K lần lượt là trung điểm của BG, BG’.
* M là trung điểm GG’⇒ BM là đường trung tuyến ΔBGG.
Mà M là trung điểm BC ⇒ BM = ½ .BC (4)
Xét ΔIGG’ và ΔNGA có:
IG = GN (chứng minh trên)
GG’ = GA (Vì G là trung điểm AG’)
⇒ ΔIGG’ = ΔNGA (c.g.c)
⇒ G’I = AN (hai cạnh tương ứng)
Mà GC = BG’ (chứng minh phần a))
⇒ Nên PG = BK.
ΔGMC = ΔG’MB (chứng minh câu a)
Xét ΔPGB và ΔKBG có:
PG = BK (chứng minh trên)
BG chung
⇒ ΔPGB = ΔKBG (c.g.c)
⇒ PB = GK (hai cạnh tương ứng)
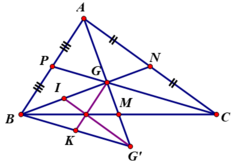
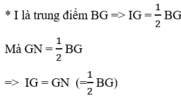
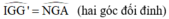
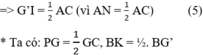
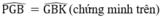
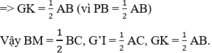
a: Ta có: G là trọng tâm
nên AG=2GD
mà AG=GM
nên GM=2GD
=>D là trung điểm của GM
Xét ΔBDM và ΔCDG có
DB=DC
góc BDM=góc CDG
DM=DG
Do đó: ΔBDM=ΔCDG
b: Ta có: ΔBDM=ΔCDG
nên BM=CG
=>BM=2/3CE