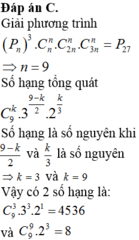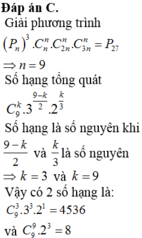Cho n là số dương.Chứng minh: T= 23n+1−23n−1+1 là hợp số
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
WG
1
KT
1

NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 1
Đặt \(A=2^{2023}+23n=8.2^{2020}+23n=8.\left(2^5\right)^{404}+23n=8.32^{404}+23n\)
Do \(32\equiv1\left(mod31\right)\Rightarrow32^{404}\equiv1\left(mod31\right)\)
\(\Rightarrow8.32^{404}\equiv8\left(mod31\right)\)
\(\Rightarrow A\) chia hết cho 31 khi và chỉ khi \(23n+8\) chia hết 31
\(\Rightarrow n=1\) là giá trị nhỏ nhất thỏa mãn
NH
0


HN
7 tháng 3 2017
Ta có: \(\dfrac{23n^2-1}{35}\in Z\)
\(\Rightarrow23n^2-1=35k\left(k\in Z\right)\)
\(\Rightarrow23n^2=35k+1\)
Mà 35k + 1 chia cho 5 hoặc 7 đều dư 1 nên 23n2 chia cho 5 hoặc 7 đều dư 1
Hay n không chia hết cho 5, 7
Vậy \(\dfrac{n}{5},\dfrac{n}{7}\) là các phân số tối giản