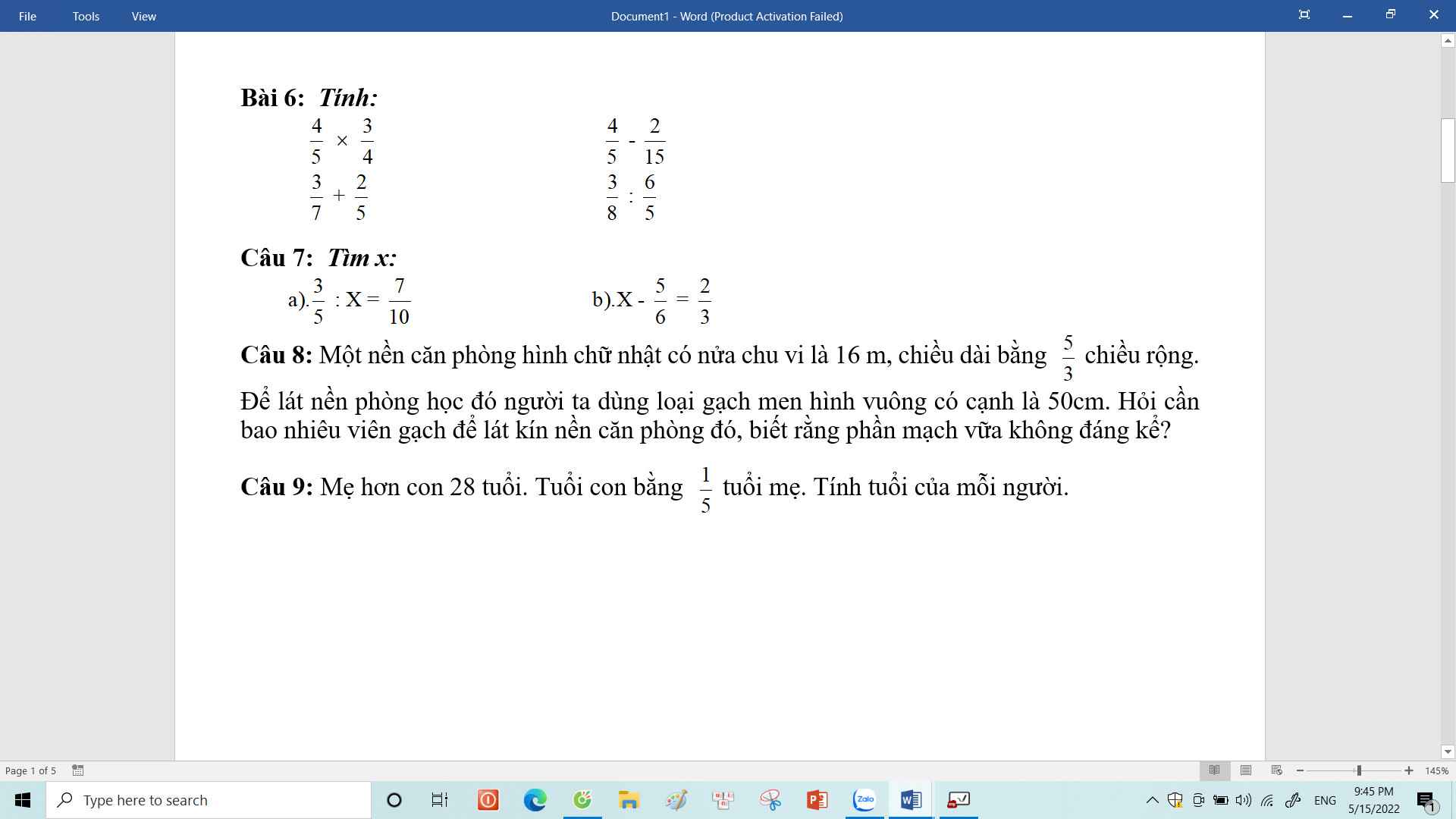
Mọi người giúp mình câu 8 với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 1
Bài 8:
a: \(x^2-4x+m-2=0\)
\(\text{Δ}=\left(-4\right)^2-4\left(m-2\right)\)
\(=16-4m+8\)
=-4m+24
Để phương trình có nghiệm thì Δ>=0
=>-4m+24>=0
=>-4m>=-24
=>\(m< =6\)
b: Theo Vi-et, ta có:
\(x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-4\right)}{1}=4\); \(x_1x_2=\dfrac{c}{a}=\dfrac{m-2}{1}=m-2\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=4^2-2\left(m-2\right)\)
\(=16-2m+4=20-2m\)
\(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(=4^2-4\left(m-2\right)\)
\(=16-4m+8=24-4m\)
\(x_1^3+x_2^3=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\)
\(=4^3-3\cdot4\cdot\left(m-2\right)\)
\(=64-12m+24=88-12m\)
NK
11 tháng 12 2021
\(\text{0,29 x 8 x 1,25 = ?}\)
\(0.29X8=2.32\)
\(2.32X1.25=\text{2.9}\)
TD
1
22 tháng 12 2020
Câu 8:
Lá gồm có phiến và cuống, trên phiến có nhiêu gai.
Lá gồm có phiến và cuống, trên phiến có nhiều gai. Phiến lá màu lục, dạng bản dẹt, là phần rộng nhất của lá, giúp hứng được nhiều ánh sáng. Có ba kiểu gân lá hình mạng, song song và hình cung.
Có hai nhóm lá chính: lá đơn và lá kép.
Lá xếp trên cây theo ba kiểu: mọc cách, mọc đối, mọc vòng. Lá trên các mấu thân xếp so le nhau giúp lá nhận được nhiều ánh sáng.
Câu 6:
b) Khi trồng đậu, bông, cà phê trước khi ra hoa tạo quả người ta thường ngắt ngọn là để cho chất dinh dưỡng dồn vào chồi hoa, nuôi quả bởi vì các cây này thu quả.c) Trồng cây lấy gỗ, lấy sợi người ta không ngắt ngọn mà tỉa cành là để cho ngọn cây phát triển, thân cây sẽ dài, sợi dài, tỉa cành xấu để cho chất dinh dưỡng tập trung nuôi thân.
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
8a.
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\left(3x^2-5x+1\right)=3-5+1=-1\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\left(-3x+2\right)=-3+2=-1\)
\(\Rightarrow\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)\Rightarrow\) hàm có giới hạn tại \(x=1\)
Đồng thời \(\lim\limits_{x\rightarrow1}f\left(x\right)=-1\)
b.
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\dfrac{x^3-8}{x-2}=\lim\limits_{x\rightarrow2^+}\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x-2}\)
\(=\lim\limits_{x\rightarrow2^+}\left(x^2+2x+4\right)=12\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\left(2x+1\right)=5\)
\(\Rightarrow\lim\limits_{x\rightarrow2^+}f\left(x\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\Rightarrow\) hàm ko có giới hạn tại x=2
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
9.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{x^2+mx+2m+1}{x+1}=\dfrac{0+0+2m+1}{0+1}=2m+1\)
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\dfrac{2x+3m-1}{\sqrt{1-x}+2}=\dfrac{0+3m-1}{1+2}=\dfrac{3m-1}{3}\)
Hàm có giới hạn khi \(x\rightarrow0\) khi:
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\Rightarrow2m+1=\dfrac{3m-1}{3}\)
\(\Rightarrow m=-\dfrac{4}{3}\)
AH
0