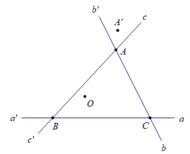
Cho nửa (O; R) đường kính AB. Gọi C là điểm chính giữa cung AB, điểm M thuộc cung AC. Hạ MH vuông góc với AB tại H, AC cắt MH tại K, MB cắt AC tại E. Hạ EI vuông góc AB tại I.
a) Chứng minh BHCK và AEMI nội tiếp.
b) Chứng minh AK.AC = AM2 và AM là tiếp tuyến của đường tròn ngoại tiếp △MKC
c) Cho R = 3cm. Tính giá trị của tổng S = AE.AC + BE.BM
d) Chứng minh khi M chuyển động trên cung AC thì tâm đường tròn ngoại tiếp △IMC luôn thuộc 1 đường cố định

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đo: ΔABC vuông tại C
Xét (O)có
ΔAMB nội tiếp
AB là đường kính
Do đo ΔAMB vuông tại M
Xét tứ giác BHKC có \(\widehat{BHK}+\widehat{BCK}=180^0\)
nên BHKC là tứ giác nội tiếp
Xét tứ giác AIEM có \(\widehat{AIE}+\widehat{AME}=180^0\)
nên AIEM là tứ giác nội tiếp
b: Xét ΔAKM và ΔAMC có
góc KAM chung
góc AMK=góc ACM
Do đó: ΔAKM\(\sim\)ΔAMC
SUy ra: AK/AM=AM/AC
hay \(AM^2=AK\cdot AC\)