Chứng minh rằng biểu thức sau không âm
x2y2 + y2z2 + z2x2 - x2yz - y2xz - z2xy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: \(=-6x^5y^6z\)
Bậc là 12
b: \(75x^2y^2+25x^2y^2=100x^2y^2\)

bn gõ bài trong công thức trực quan ik, khó nhìn lắm, ko làm đc
1). x2y2(y-x)+y2z2(z-y)-z2x2(z-x)
2)xyz-(xy+yz+xz)+(x+y+z)-1
3)yz(y+z)+xz(z-x)-xy(x+y)
5)y(x-2z)2+8xyz+x(y-2z)2-2z(x+y)2
6)8x3(y+z)-y3(z+2x)-z3(2x-y)
7) (x2+y2)3+(z2-x2)3-(y2+z2)3

Ta có :
\(C=2x^2+y^2-2xy-10x+27\)
\(=\left(x^2+y^2-2xy\right)+\left(x^2-10x+25\right)+2\)
\(=\left(x-y\right)^2+\left(x-5\right)^2+2\)
Ta có :
\(\left(x-y\right)^2\ge0\)
\(\left(x-5\right)^2\ge0\)
\(\Rightarrow\left(x-y\right)^2+\left(x-5\right)^2+2\ge2>0\)
\(\Rightarrow C>0\)
Vậy ...

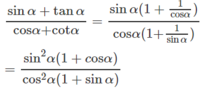
Vì 1 + cosα ≥ 0 và 1 + sinα ≥ 0 cho nên biểu thức đã cho không thể có giá trị là một số âm.
\(\Leftrightarrow\left\{{}\begin{matrix}a=xy;b=yz;c=zx\\A=a^2+b^2+c^2-ab-bc-ac\end{matrix}\right.\)
\(2A=\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\)
2A là tổng 3 số không âm => 2A không âm => A không âm
đẳng thức khi a=b=c <=> x=y=z
=> dpcm